��Ŀ����
����Ŀ����ͼ1��������y=�� ![]() [��x��2��2+n]��x�ύ�ڵ�A��m��2��0����B��2m+3��0������A�ڵ�B����ࣩ����y�ύ�ڵ�C������BC��
[��x��2��2+n]��x�ύ�ڵ�A��m��2��0����B��2m+3��0������A�ڵ�B����ࣩ����y�ύ�ڵ�C������BC��
��1����m��n��ֵ��
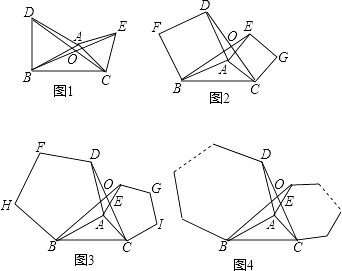
��2����ͼ2����NΪ�������ϵ�һ���㣬��λ��ֱ��BC�Ϸ�������CN��BN�����NBC��������ֵ��
��3����ͼ3����M��P�ֱ�Ϊ�߶�BC���߶�OB�ϵĶ��㣬����PM��PC���Ƿ���������ĵ�P��ʹ��PCMΪ���������Σ���PMBΪֱ��������ͬʱ�����������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�������ߵĽ���ʽΪy=�� ![]() [��x��2��2+n]=��
[��x��2��2+n]=�� ![]() ��x��2��2��
��x��2��2�� ![]() n��
n��
�������ߵĶԳ���Ϊֱ��x=2��
�ߵ�A�͵�BΪ�ԳƵ㣬
��2����m��2��=2m+3��2�����m=1��
��A����1��0����B��5��0����
��A����1��0������y=�� ![]() [��x��2��2+n]��9+n=0�����n=��9
[��x��2��2+n]��9+n=0�����n=��9
��2��
�⣺��ND��y�ύBC��D����ͼ2��

�����߽���ʽΪy=�� ![]() [��x��2��2��9]=��
[��x��2��2��9]=�� ![]() x2+
x2+ ![]() x+3��
x+3��
��x=0ʱ��y=3����C��0��3����
��ֱ��BC�Ľ���ʽΪy=kx+b��
��B��5��0����C��0��3������� ![]() �����
����� 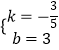 ��
��
��ֱ��BC�Ľ���ʽΪy=�� ![]() x+3��
x+3��
��N��x���� ![]() x2+
x2+ ![]() x+3������D��x����
x+3������D��x���� ![]() x+3����
x+3����
��ND=�� ![]() x2+
x2+ ![]() x+3������
x+3������ ![]() x+3��=��
x+3��=�� ![]() x2+3x��
x2+3x��
��S��NBC=S��NDC+S��NDB= ![]() 5ND=��
5ND=�� ![]() x2+
x2+ ![]() x=����x��
x=����x�� ![]() ��2+
��2+ ![]() ��
��
��x= ![]() ʱ����NBC���������ֵΪ
ʱ����NBC���������ֵΪ ![]()
��3��
�⣺���ڣ�
��B��5��0����C��0��3����
��BC= ![]() =
= ![]() ��
��
����PMB=90�㣬���PMC=90�㣬��PMCΪ����ֱ�������Σ�MP=MC��
��PM=t����CM=t��MB= ![]() ��t��
��t��
�ߡ�MBP=��OBC��
���BMP�ס�BOC��
�� ![]() =
= ![]() =
= ![]() ����
���� ![]() =
= ![]() =
= ![]() �����t=
�����t= ![]() ��BP=
��BP= ![]() ��
��
��OP=OB��BP=5�� ![]() =
= ![]() ��
��
��ʱP������Ϊ�� ![]() ��0����
��0����
����MPB=90�㣬��MP=MC��
��PM=t����CM=t��MB= ![]() ��t��
��t��
�ߡ�MBP=��CBO��
���BMP�ס�BCO��
�� ![]() =
= ![]() =
= ![]() ����
���� ![]() =
= ![]() =
= ![]() �����t=
�����t= ![]() ��BP=
��BP= ![]() ��
��
��OP=OB��BP=5�� ![]() =
= ![]() ��
��
��ʱP������Ϊ�� ![]() ��0����
��0����
����������P�������� ![]() ��0����
��0���� ![]() ��0����
��0����

����������1�����������ߵĽ���ʽȷ���Գ���Ϊֱ��x=2�������öԳ��Եõ�2����m��2��=2m+3��2���ⷽ�̿ɵ�m��ֵ���Ӷ��õ�A����1��0����B��5��0����Ȼ���A���������y=�� ![]() [��x��2��2+n]�����n��ֵ����2����ND��y�ύBC��D����ͼ2�����������߽���ʽȷ��C��0��3���������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=��
[��x��2��2+n]�����n��ֵ����2����ND��y�ύBC��D����ͼ2�����������߽���ʽȷ��C��0��3���������ô���ϵ�������ֱ��BC�Ľ���ʽΪy=�� ![]() x+3����N��x����
x+3����N��x���� ![]() x2+
x2+ ![]() x+3������D��x����
x+3������D��x���� ![]() x+3�������������������ʽ������S��NBC=S��NDC+S��NDB�ɵ�S��BCN=��
x+3�������������������ʽ������S��NBC=S��NDC+S��NDB�ɵ�S��BCN=�� ![]() x2+
x2+ ![]() x��Ȼ�����ö��κ�����������⣻��3�������ù��ɶ��������BC=
x��Ȼ�����ö��κ�����������⣻��3�������ù��ɶ��������BC= ![]() ���ٷ������ۣ�����PMB=90�㣬���PMC=90�㣬��PMCΪ����ֱ�������Σ�MP=MC����PM=t����CM=t��MB=
���ٷ������ۣ�����PMB=90�㣬���PMC=90�㣬��PMCΪ����ֱ�������Σ�MP=MC����PM=t����CM=t��MB= ![]() ��t��֤����BMP�ס�BOC���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����ꣻ����MPB=90�㣬��MP=MC����PM=t����CM=t��MB=
��t��֤����BMP�ס�BOC���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����ꣻ����MPB=90�㣬��MP=MC����PM=t����CM=t��MB= ![]() ��t��֤����BMP�ס�BCO���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����꣮���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ�����������Ͷ��κ��������ʣ������ô���ϵ������������ʽ������������ͼ�ε����ʣ��������������ε��ж������������Ʊȼ����߶εij����ʾ�߶�֮��Ĺ�ϵ��ѧ�����÷������۵�˼������ѧ���⣮
��t��֤����BMP�ס�BCO���������Ʊȿ����BP�ij����ټ���OP��ɵõ�P�����꣮���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ�����������Ͷ��κ��������ʣ������ô���ϵ������������ʽ������������ͼ�ε����ʣ��������������ε��ж������������Ʊȼ����߶εij����ʾ�߶�֮��Ĺ�ϵ��ѧ�����÷������۵�˼������ѧ���⣮
�����㾫����������Ҫ�����˶��κ��������ʺͱ����߶ε����֪ʶ�㣬��Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С�����ѡ��ͬһ���ȵ�λ���������߶�a��b�ij��ȷֱ�Ϊm��n����ô��˵�������߶εı���a/b=m/n����д��a��b=m��n������ȷ�����⣮