题目内容
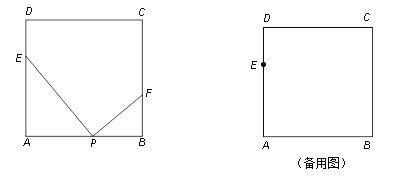
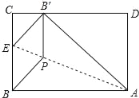
【题目】将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B'作B'P∥BC,交AE于点P,连接BP.已知BC=3,CB'=1,下列结论:①AB=5;②sin∠ABP=![]() ;③四边形BEB′P为菱形;④S四边形BEB'P﹣S△ECB'=1,其中正确的个数是( )
;③四边形BEB′P为菱形;④S四边形BEB'P﹣S△ECB'=1,其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
(1)根据翻折的性质和勾股定理列方程求解,①正确;
(2)根据翻折的性质和B′P∥BC证明B′P=BE,四边形BEB′P为平行四边形,再由BE=B′E,四边形BEB′P为菱形,③正确;
(3)延长B′P与AB交于点M,则PM⊥AB,根据勾股定理得到BE,进而求出BP、PM,sin∠ABP=![]() ;故②错误;
;故②错误;
(4)S四边形BEB′P-S△ECB′=BE×CB′-![]() CE×CB′=1,④正确.
CE×CB′=1,④正确.
(1)设AB=CD=x,根据翻折的性质AB=AB′=x,B′D=x-1,AD=3
∴x2=(x-1)2+32,
解得:x=5,
∴①正确;
(2)∵B′P∥BC,
∴∠BEP=∠B′PE,
根据翻折的性质∠BEP=∠B′EP,
∴∠B′EP=∠B′PE,
∴B′E=B′P,
∵BE=B′E,
∴BE=B′P,
∴四边形BEB′P为菱形,
∴③正确;
(3)延长B′P与AB交于点M,则PM⊥AB,

设BE=m,则CE=3-m,CB′=1,
∴m2=(3-m)2+12,
解得:m=![]() ,
,
∴BE=BP=B′P=![]() ,
,
∴CE=PM=![]() ,
,
∴sin∠ABP=![]() ,
,
∴②错误;
(4)S四边形BEB′P-S△ECB′=BE×CB′-![]() CE×CB′=
CE×CB′=![]() ×1-
×1-![]() ×
×![]() ×1=1,
×1=1,
∴④正确.
故选C.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目