题目内容
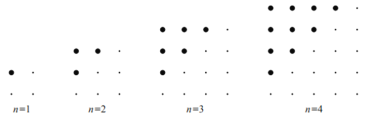
【题目】在下图中,每个正方形点阵由大点和小点组成:
(1)第7个正方形点阵中,大点和小点的总共的个数是________其中大点的个数是_________.
(2)第n个图形中,大点的个数是__________;(用含n的式子表示)
(3)是否存在某个图形,使得大点的个数是210个?若存在,请求出n的值,若不存在,请说明理由.
【答案】(1)64;28;(2)![]() ;(3)第20个图形大点的个数是210个.
;(3)第20个图形大点的个数是210个.
【解析】
(1)(2)可以通过列表找规律的方法,找出相应的点的个数;
(3)通过方程![]() ,求解即可.
,求解即可.
(1)
依照题意,可得下表:
图形 | 大点个数 | 大点和小点的总共个数 |
第1个 | 1 |
|
第2个 | 3=1+2 |
|
第3个 | 6=1+2+3 |
|
┄ | ┄ | ┄ |
第7个 | 1+2+3+4+5+6+7=28 |
|
(2)由(1)图标可知第n个图形中,大点的个数是:![]()
(3)当大点的个数是210个时,即![]() ,
,
∴![]()
解之得:![]() 或
或![]() (不合题意,舍去)
(不合题意,舍去)
所以存在第20个图形,使得大点的个数是210个.

练习册系列答案
相关题目
【题目】如表:方程1、方程2、方程3、…是按一定规律排列的一列方程.
序号 | 方程 | 方程的解 | |
1 | x2+x﹣2﹣=0 | x1=﹣2 | x2=1 |
2 | x2+2x﹣8﹣=0 | x1=﹣4 | x2=2 |
3 | x2+3x﹣18=0 | x1= | x2= |
… | … | … | … |
(1)解方程3,并将它的解填在表中的空白处;
(2)请写出这列方程中第10个方程,并用求根公式求其解.
(3)根据表中的规律写出第n个方程和这个方程的解.