题目内容
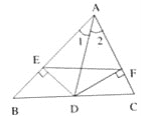
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() 分别在正方形的四条边上,且
分别在正方形的四条边上,且![]() ,则四边形
,则四边形![]() 的形状为________,它的面积的最小值为________.
的形状为________,它的面积的最小值为________.

【答案】正方形![]()
【解析】
先证明△AEH≌△DFE≌△CGF≌△BHG,从而得到HE=EF=FG=HG,然后证明EFGH四边形有一个角是直角,从而可判断出四边形EFGH的形状,设AE=x,则AH=(![]() -x),依据正方形的面积公式以及勾股定理可得到四边形EFGH的面积与x的函数关系式,依据二次函数的性质求得二次函数的最小值即可.
-x),依据正方形的面积公式以及勾股定理可得到四边形EFGH的面积与x的函数关系式,依据二次函数的性质求得二次函数的最小值即可.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD, ∠A=∠B=∠C=∠D.
∵AE=DF=CG=BH,
∴AH=ED=FG=BG.
在△AEH、△DFE、△CGF、△BHG中,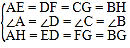 ,
,
∴△AEH≌△DFE≌CGF≌△BHG.
∴HE=EF=FG=HG.
∴四边形EFGH是菱形.
∵△AEH≌△DFE,
∴∠AEH=∠DFE.
∵∠AHE+∠AEH=90°,
∴∠DEF+∠AEH=90°.
∴∠HEF=90°.
∴EHGF为正方形.
设AE=x,则AH=(![]() -x).
-x).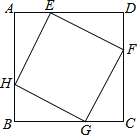
∵正方形EFHG的面积=HE=AE+AH=x+(![]() -x) =2x-2
-x) =2x-2![]() x+5,
x+5,
∴当x=![]() 时,正方形的面积有最小值.
时,正方形的面积有最小值.
∴正方形EFHG的面积的最小值=![]() .
.
故答案为:正方形;![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目