Question

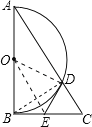
【题目】如图，Rt△ABC中，∠ABC=90°，以AB为直径作半圆⊙O交AC与点D，点E为BC的中点，连接DE．

（1）求证：DE是半圆⊙O的切线．

（2）若∠BAC=30°，DE=2，求AD的长．

Answer 1

【答案】（1）见解析；（2）6

【解析】

试题分析：（1）连接OD，OE，由AB为圆的直径得到三角形BCD为直角三角形，再由E为斜边BC的中点，得到DE=BE=DC，再由OB=OD，OE为公共边，利用SSS得到三角形OBE与三角形ODE全等，由全等三角形的对应角相等得到DE与OD垂直，即可得证；

（2）在直角三角形ABC中，由∠BAC=30°，得到BC为AC的一半，根据BC=2DE求出BC的长，确定出AC的长，再由∠C=60°，DE=EC得到三角形EDC为等边三角形，可得出DC的长，由AC﹣CD即可求出AD的长．

（1）证明：连接OD，OE，BD，

∵AB为圆O的直径，

∴∠ADB=∠BDC=90°，

在Rt△BDC中，E为斜边BC的中点，

∴DE=BE，

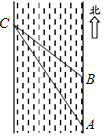
在△OBE和△ODE中，

，

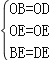∴△OBE≌△ODE（SSS），

∴∠ODE=∠ABC=90°，

则DE为圆O的切线；

（2）在Rt△ABC中，∠BAC=30°，

∴BC=AC，

∵BC=2DE=4，

∴AC=8，

又∵∠C=60°，DE=CE，

∴△DEC为等边三角形，即DC=DE=2，

则AD=AC﹣DC=6．