Question

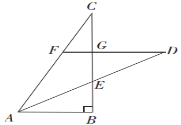
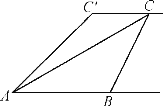
【题目】如图所示，小敏、小亮从A，B两地观测空中C处一个气球，分别测得仰角为30°和60°，A，B两地相距100 m．当气球沿与BA平行地方向飘移10 s后到达C′处时，在A处测得气球的仰角为45°.

(1)求气球的高度(保留根式)；

(2)求气球飘移的平均速度(保留根式)．

Answer 1

【答案】（1）CD＝50 m.（2）（15－5） m/s.

【解析】

（1）分别过C、C′作AB的垂线，设垂足为D、E；在Rt△ACD和Rt△BCD中，利用所给角的三角函数分别用BD表示出CD，联立两式即可求出CD、BD的长．

（2）直角梯形ADCC′中，已知了BD、AB的长，即可求出AD的长；而AE的长可在Rt△AEC′中利用已知角的三角函数求出，即可得出ED、CC′的长，也就得出了气球10秒漂移的距离，根据速度=路程÷时间，即可得解．

解：（1）如答图所示，作CD⊥AB，C′E⊥AB，垂足分别为D，E.

∵CD＝BD·tan60°，CD＝(100＋BD)·tan30°，

∴(100＋BD)·tan30°＝BD·tan60°，

∴BD＝50(m)，CD＝50(m)，

∴气球的高度约为CD＝50m.

（2）∵BD＝50 m，AB＝100 m，

∴AD＝150 m，

又∵AE＝C′E＝50m，

∴DE＝（150－50）m，

（150－50）÷10＝（15－5）(m/s)．

∴气球飘移的平均速度约为（15－5） m/s.