Question

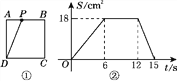
【题目】如图①所示，正方形ABCD的边长为6 cm，动点P从点A出发，在正方形的边上沿A→B→C→D运动，设运动的时间为t(s)，三角形APD的面积为S(cm2)，S与t的函数图象如图②所示，请回答下列问题：

(1)点P在AB上运动的时间为________s，在CD上运动的速度为________cm/s，三角形APD的面积S的最大值为________cm2；

(2)求出点P在CD上运动时S与t之间的函数表达式；

(3)当t为何值时，三角形APD的面积为10 cm2?

Answer 1

【答案】(1)6；2；18(2) S＝90－6t(12≤t≤15)(3) 10cm2

【解析】试题分析：（1）直接根据函数图象上坐标可求出点P在AB上运动的速度为 6÷6=1cm/s，在CD上运动的速度为 6÷3=2cm/s；

（2）用t表示PD=6-2（t-12）=30-2t，代入面积公式可求S=90-6t；

（3）通过图象可知，△APD的面积为10cm2．即S=10，分别在S=3t和S=90-6t，上代入即可求得t=，t=．

试题解析：（1）点P在AB上运动的速度为6÷6=1cm/s，在CD上运动的速度为6÷3=2cm/s，

当点P运动到点B时，△APD的面积S最大，最大值是×6×6=18cm2；

（2）PD=62(t12)=302t，

S=ADPD=×6×(302t)=906t；

（3）当0t6时，S=3t，

△APD的面积为10cm2，即S=10时，

3t=10，t=，

当12t15时，906t=10，t=，

所以当t为秒、秒时，△APD的面积为10cm2.