题目内容
(2005•南宁)OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=6.(1)如图,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作B'点.求B'点的坐标;
(2)求折痕CM所在直线的解析式;
(3)作B'G∥AB交CM于点G,若抛物线y=
 x2+m过点G,求抛物线的解析式,并判断以原点O为圆心,OG为半径的圆与抛物线除交点G外,是否还有交点?若有,请直接写出交点的坐标.
x2+m过点G,求抛物线的解析式,并判断以原点O为圆心,OG为半径的圆与抛物线除交点G外,是否还有交点?若有,请直接写出交点的坐标.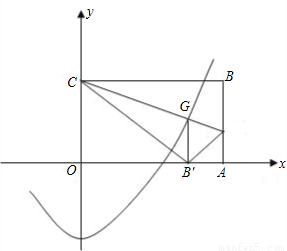
【答案】分析:(1)求B′的坐标就是求OB′的长,也就要知道CB′的长,而根据折叠的性质可知CB′=CB,而四边形OCBA是矩形,可得出CB=OA,、,也就得出了CB′=OA,即可求出OB′的长,也就求出了B′的坐标;
(2)求CM所在直线的解析式,根据OC的长可得出C的坐标,关键是求M点的坐标,M的横坐标与A的横坐标相同,那么就要求出M的纵坐标即AM的长,(1)中已求得了OB′的长,也就求出了AB′的长,可用AM表示出MB也就是MB′的长,然后在直角三角形AB′M中用勾股定理求出AM的长,也就得出了M的坐标,然后用待定系数法求出CM所在直线的解析式.
(3)(1)中已经求得了OB′的长,也就是G的横坐标,然后代入CM所在直线的解析式中求出G点的坐标,然后代入抛物线的解析式中求出m的值,即可得出抛物线的解析式.根据抛物线和圆的对称性可得出抛物线与圆的另外一个交点就应该是G关于y轴的对称点.
解答:解:(1)∵△CB'M≌△CBM
∴CB'=CB=OA=10
∴OB'=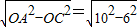 =8
=8
∴B'(8,0);
(2)设AM=n,则MB'=BM=6-n
AB'=10-8=2
∴n2+22=(6-n)2
解得n= .
.
∴M(10, )、C(0,6)
)、C(0,6)
设直线CM解析式为y=kx+b
∴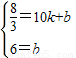
解得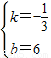
∴直线CM的解析式为y=- x+6;
x+6;
(3)设G(8,a)
∴a=- ×8+6=
×8+6=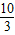
∴G(8,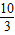 )
)
∴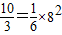 +m
+m
∴m=-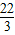
∴y= x2-
x2-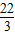
除交点G外,另有交点为点G关于y轴的对称点.
其坐标为(-8,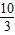 ).
).
点评:本题主要考查了折叠的性质,矩形的性质,一次函数的应用,以及用待定系数法求二次函数解析式等知识点.
(2)求CM所在直线的解析式,根据OC的长可得出C的坐标,关键是求M点的坐标,M的横坐标与A的横坐标相同,那么就要求出M的纵坐标即AM的长,(1)中已求得了OB′的长,也就求出了AB′的长,可用AM表示出MB也就是MB′的长,然后在直角三角形AB′M中用勾股定理求出AM的长,也就得出了M的坐标,然后用待定系数法求出CM所在直线的解析式.
(3)(1)中已经求得了OB′的长,也就是G的横坐标,然后代入CM所在直线的解析式中求出G点的坐标,然后代入抛物线的解析式中求出m的值,即可得出抛物线的解析式.根据抛物线和圆的对称性可得出抛物线与圆的另外一个交点就应该是G关于y轴的对称点.
解答:解:(1)∵△CB'M≌△CBM
∴CB'=CB=OA=10
∴OB'=
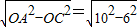 =8
=8∴B'(8,0);
(2)设AM=n,则MB'=BM=6-n
AB'=10-8=2
∴n2+22=(6-n)2
解得n=
 .
.∴M(10,
 )、C(0,6)
)、C(0,6)设直线CM解析式为y=kx+b
∴
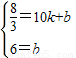
解得
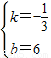
∴直线CM的解析式为y=-
 x+6;
x+6;(3)设G(8,a)
∴a=-
 ×8+6=
×8+6=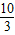
∴G(8,
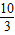 )
)∴
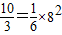 +m
+m∴m=-
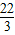
∴y=
 x2-
x2-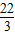
除交点G外,另有交点为点G关于y轴的对称点.
其坐标为(-8,
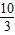 ).
).点评:本题主要考查了折叠的性质,矩形的性质,一次函数的应用,以及用待定系数法求二次函数解析式等知识点.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
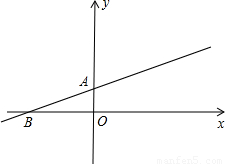
 x2+m过点G,求抛物线的解析式,并判断以原点O为圆心,OG为半径的圆与抛物线除交点G外,是否还有交点?若有,请直接写出交点的坐标.
x2+m过点G,求抛物线的解析式,并判断以原点O为圆心,OG为半径的圆与抛物线除交点G外,是否还有交点?若有,请直接写出交点的坐标.