题目内容
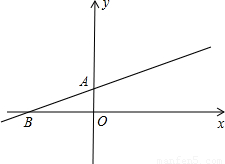
(2005•南宁)直线y=kx+b经过点A(0,1),B(-3,0),点P是这条直线上的一个动点,以P为圆心的圆与x轴相切于点C.(1)求直线AB的解析式;
(2)设点P的横坐标为t,若⊙P与y轴相切,求t的值;
(3)是否存在点P,使⊙P与y轴两交点间的距离恰好等于2?若存在,求出点P的坐标;若不存在,请说明理由.
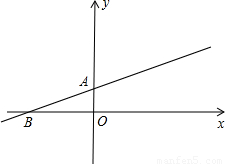
【答案】分析:(1)可以用待定系数法确定直线AB的解析式;
(2)根据P为圆心的圆与x轴相切,也与y轴相切得到它到两坐标轴的距离相等,设P的横坐标为t,就可以列出关于t的方程,解方程就可以求出t;
(3)如图,首先根据垂径定理得M是CD的中点,然后根据勾股定理计算t的值就可以求出t了.
解答:解:(1)直线AB的解析式为y=kx+b,
∴ ,
,
∴k= ,b=1,
,b=1,
∴y= x+1;
x+1;
(2)设P(t, t+1),
t+1),
∵以P为圆心的圆与x轴相切,且⊙P与y轴相切,
∴t= t+1或-t=
t+1或-t= t+1,
t+1,
∴t= 或t=-
或t=- ;
;
(3)假设P点存在,
设其坐标为:P(t, t+1),
t+1),
过P作PM⊥CD于M,PN⊥x轴于N,连接PC,
则PN=PC= t+1,PM=t,根据已知CD=2,则CM=1,
t+1,PM=t,根据已知CD=2,则CM=1,
∴PC2=PM2+CM2,
∴ ,
,
∴t1=0,t2= ,
,
∴P(0,1)或P( ,
, ).
).
点评:此题把圆的知识与一次函数,勾股定理结合起来,综合考查了这几方面的知识,有一定的综合性.
(2)根据P为圆心的圆与x轴相切,也与y轴相切得到它到两坐标轴的距离相等,设P的横坐标为t,就可以列出关于t的方程,解方程就可以求出t;
(3)如图,首先根据垂径定理得M是CD的中点,然后根据勾股定理计算t的值就可以求出t了.
解答:解:(1)直线AB的解析式为y=kx+b,
∴
 ,
,∴k=
 ,b=1,
,b=1,∴y=
 x+1;
x+1;(2)设P(t,
 t+1),
t+1),∵以P为圆心的圆与x轴相切,且⊙P与y轴相切,
∴t=
 t+1或-t=
t+1或-t= t+1,
t+1,∴t=
 或t=-
或t=- ;
;(3)假设P点存在,

设其坐标为:P(t,
 t+1),
t+1),过P作PM⊥CD于M,PN⊥x轴于N,连接PC,
则PN=PC=
 t+1,PM=t,根据已知CD=2,则CM=1,
t+1,PM=t,根据已知CD=2,则CM=1,∴PC2=PM2+CM2,
∴
 ,
,∴t1=0,t2=
 ,
,∴P(0,1)或P(
 ,
, ).
).点评:此题把圆的知识与一次函数,勾股定理结合起来,综合考查了这几方面的知识,有一定的综合性.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 x2+m过点G,求抛物线的解析式,并判断以原点O为圆心,OG为半径的圆与抛物线除交点G外,是否还有交点?若有,请直接写出交点的坐标.
x2+m过点G,求抛物线的解析式,并判断以原点O为圆心,OG为半径的圆与抛物线除交点G外,是否还有交点?若有,请直接写出交点的坐标.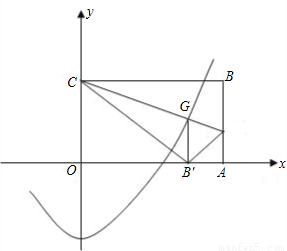
 x2+m过点G,求抛物线的解析式,并判断以原点O为圆心,OG为半径的圆与抛物线除交点G外,是否还有交点?若有,请直接写出交点的坐标.
x2+m过点G,求抛物线的解析式,并判断以原点O为圆心,OG为半径的圆与抛物线除交点G外,是否还有交点?若有,请直接写出交点的坐标.