题目内容
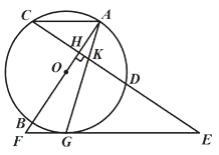
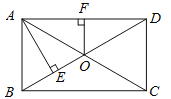
【题目】如图所示,矩形ABCD的对角线相交于点O,OF⊥AD于点F,OF=2cm,AE⊥BD于点E,且BE﹕BD=1﹕4,求AC的长.
【答案】8cm
【解析】试题分析:根据矩形的对角线相等且互相平分可得OA=OB,根据比例设BE=x,表示出BD=4x,然后求出BE=OE,从而判断出△ABO是等边三角形,然后判断出OE是△AOD的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半求出AB,再求解即可.
试题解析:∵四边形ABCD为矩形,
∴∠BAD=90°,OB=OD,AC=BD,
又∵OF⊥AD,
∴OF∥AB,
又∵OB=OD ,
∴ AB=2OF=4cm,
∵BE︰BD=1︰4,
∴BE︰ED=1︰3
设BE=x,ED=3x ,
则BD=4 x ,
∵AE⊥BD于点E
∴![]() ,
,
∴16-x2=AD2-9x2
又∵AD2=BD2-AB2=16 x2-16 ,
∴16-x2=16 x2-16-9x2,8x2=32
∴x2=4,
∴x=2
∴BD=2×4=8(cm),
∴AC=8cm .

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目