题目内容
我国宋代数学家杨辉在1261年提到一个有意思的关于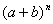 展开式中各项系数间的关系:
展开式中各项系数间的关系:

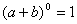 ,它只有一项,系数为1;
,它只有一项,系数为1;
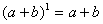 ,它有两项,系数为1、1;
,它有两项,系数为1、1;
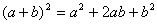 ,它有三项,系数为1、2、1;
,它有三项,系数为1、2、1;
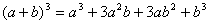 ,它有四项,系数为1、3、3、1;
,它有四项,系数为1、3、3、1;
如果把其系数按上图排列,得到一个三角形,我们把它叫杨辉三角,其规律的发现比欧洲早393年;那么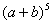 展开项的所有系数的和为 ( )
展开项的所有系数的和为 ( )
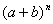 展开式中各项系数间的关系:
展开式中各项系数间的关系:
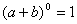 ,它只有一项,系数为1;
,它只有一项,系数为1;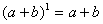 ,它有两项,系数为1、1;
,它有两项,系数为1、1;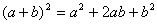 ,它有三项,系数为1、2、1;
,它有三项,系数为1、2、1;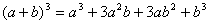 ,它有四项,系数为1、3、3、1;
,它有四项,系数为1、3、3、1; 如果把其系数按上图排列,得到一个三角形,我们把它叫杨辉三角,其规律的发现比欧洲早393年;那么
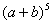 展开项的所有系数的和为 ( )
展开项的所有系数的和为 ( )| A.16 | B.22 | C.32 | D.64 |
C
试题分析:仔细分析所给式子的特征可得
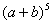 展开项有六项,系数分别为1、5、10、10、5、1,即可求得结果.
展开项有六项,系数分别为1、5、10、10、5、1,即可求得结果.由题意得
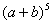 展开项的所有系数的和为
展开项的所有系数的和为
故选C.
点评:解答此类问题的关键是仔细分析所给式子的特征得到规律,再把发现的规律应用于解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
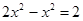
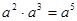
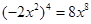
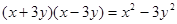
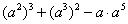 (2)
(2) 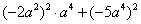
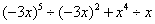 (4)
(4) 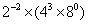
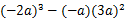 (6)
(6)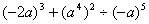
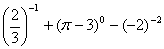 ; (8) (0.125)2008.(-8)2009
; (8) (0.125)2008.(-8)2009 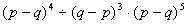
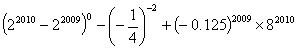
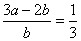 ,那么
,那么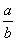 的值为______。
的值为______。 ,把多项式
,把多项式 因式分解。
因式分解。 ,其中
,其中