题目内容
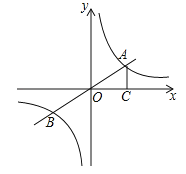
【题目】如图,直线y=kx(k为常数,k≠0)与双曲线![]() (m为常数,m>0)的交点为A、B,AC⊥x轴于点C,∠AOC=30°,OA=2.
(m为常数,m>0)的交点为A、B,AC⊥x轴于点C,∠AOC=30°,OA=2.
(1)求m的值;
(2)点P在y轴上,如果![]() ,求P点的坐标.
,求P点的坐标.
【答案】(1)![]() ;(2)P(0,1)或(0,﹣1).
;(2)P(0,1)或(0,﹣1).
【解析】
试题分析:(1)求出点A坐标利用待定系数法即可解决问题;
(2)设P(0,n),由A(![]() ,1),B(﹣
,1),B(﹣![]() ,﹣1),可得
,﹣1),可得![]() |n|
|n|![]() +
+![]() |n|
|n|![]() =3×
=3×![]() ,解方程即可;
,解方程即可;
试题解析:(1)在Rt△AOC中,∵∠ACO=90°,∠AOC=30°,OA=2,∴AC=1,OC=![]() ,∴A(
,∴A(![]() ,1),∵反比例函数
,1),∵反比例函数![]() 经过点A(
经过点A(![]() ,1),∴m=
,1),∴m=![]() ,∵y=kx经过点A(
,∵y=kx经过点A(![]() ,1),∴k=
,1),∴k=![]() .
.
(2)设P(0,n),∵A(![]() ,1),B(﹣
,1),B(﹣![]() ,﹣1),∴
,﹣1),∴![]() |n|
|n|![]() +
+![]() |n|
|n|![]() =3×
=3×![]() ,∴n=±1,∴P(0,1)或(0,﹣1).
,∴n=±1,∴P(0,1)或(0,﹣1).

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目