题目内容
【题目】如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤![]() PD=EC.其中有正确有( )个.
PD=EC.其中有正确有( )个.

A. 2B. 3C. 4D. 5
【答案】D
【解析】
过P作PG⊥AB于点G,根据正方形对角线的性质及题中的已知条件,证明△AGP≌△FPE后即可证明①AP=EF;④∠PFE=∠BAP;在此基础上,根据正方形的对角线平分对角的性质,在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,求得DP=![]() EC,得出⑤正确,即可得出结论.
EC,得出⑤正确,即可得出结论.
过P作PG⊥AB于点G,如图所示:
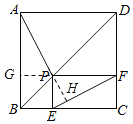
∵点P是正方形ABCD的对角线BD上一点,
∴GP=EP,
在△GPB中,∠GBP=45°,
∴∠GPB=45°,
∴GB=GP,
同理:PE=BE,
∵AB=BC=GF,
∴AG=AB-GB,FP=GF-GP=AB-GB,
∴AG=PF,
在△AGP和△FPE中,
 ,
,
∴△AGP≌△FPE(SAS),
∴AP=EF,①正确,∠PFE=∠GAP,
∴∠PFE=∠BAP,④正确;
延长AP到EF上于一点H,
∴∠PAG=∠PFH,
∵∠APG=∠FPH,
∴∠PHF=∠PGA=90°,
∴AP⊥EF,②正确,
∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45°,
∴当∠PAD=45°或67.5°时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,故③正确.
∵GF∥BC,
∴∠DPF=∠DBC,
又∵∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,
∴PF=EC,
∴在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,
∴DP=![]() EC,
EC,
即![]() PD=EC,⑤正确.
PD=EC,⑤正确.
∴其中正确结论的序号是①②③④⑤,共有5个.
故选D.