题目内容
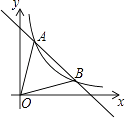
【题目】如图,对于二次函数y=ax2+bx+c(a≠0)的图象,得出了下面五条信息:①c>0;②b=6a;③b2﹣4ac>0;④a+b+c<0;⑤对于图象上的两点(﹣6,m )、(1,n),有m<n.其中正确信息的个数有( )
A.2个
B.3个
C.4个
D.5个
【答案】C
【解析】解:因为函数图象与y轴的交点在y轴的正半轴可知,
所以c>0,∴①正确;
∵函数的对称轴为x=﹣ ![]() =
= ![]() =﹣3,
=﹣3,
∴b=6a,∴②正确;
抛物线与x轴有两个交点,
∴b2﹣4ac>0,∴③正确;
当x=1时,y>0,
∴a+b+c>0,∴④错误;
∵对称轴为x=﹣3,|﹣6﹣(﹣3)|=3,|1﹣(﹣3)|=4,
∴m<n,∴⑤正确.
其中正确信息的有①②③⑤,
所以答案是:C.
【考点精析】通过灵活运用二次函数图象以及系数a、b、c的关系,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)即可以解答此题.

 53随堂测系列答案
53随堂测系列答案【题目】某班要从甲、乙两名同学中选拔出一人,代表班级参加学校的一分钟踢毽子体能素质比赛,在一段时间内的相同条件下,甲、乙两人进行了六场一分钟踢毽子的选拔测试,根据他们的成绩绘制出如图的统计表和不完整的折线统计图.
甲、乙两人选拔测试成绩统计表
甲成绩 | 乙成绩 | |
第1场 | 87 | 87 |
第2场 | 94 | 98 |
第3场 | 91 | 87 |
第4场 | 85 | 89 |
第5场 | 91 | 100 |
第6场 | 92 | 85 |
中位数 | 91 | n |
平均数 | m | 91 |
并计算出乙同学六场选拔测试成绩的方差:
S乙2= ![]() =
= ![]()
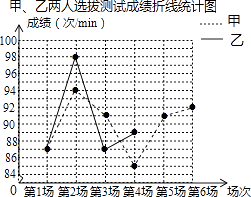
(1)m= , n= , 并补全全图中甲、乙两人选拔测试成绩折线统计图;
(2)求甲同学六场选拔测试成绩的方差S甲2;
(3)分别从平均数、中位数和方差的角度分析比较甲、乙二人的成绩各有什么特点?
(4)经查阅该校以往本项比赛的资料可知,①成绩若达到90次/min,就有可能夺得冠军,你认为选谁参赛更有把握夺冠?为什么?
②该项成绩的最好记录是95次/min,就有可能夺得冠军,你认为选谁参赛更有把握夺冠?为什么?