题目内容
【题目】如图,在△ABC中,AB=AC,∠BAC=90,BD是![]() 的平分线,CE⊥BD,垂足是E,BA和CE的延长线交于点F.
的平分线,CE⊥BD,垂足是E,BA和CE的延长线交于点F.
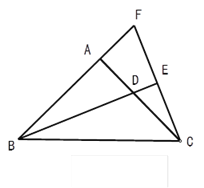
(1)在图中找出与△ABD全等的三角形,并说出全等的理由;
(2)说明BD=2EC;
(3)如果AB=5,BC=5![]() 求AD的长.
求AD的长.
【答案】(1)理由见解析;(2)理由见解析;(3) 5![]() 5.
5.
【解析】分析(1)可利用ASA判断△ABD≌△ACF;(2)根据(1)可得BD=CF,证明△BFE≌△BCE,可得出EF=CE=![]() CF,继而可得出结论;(3)过D作DM⊥BC,设AD=DM=MC=x,则可得DC=
CF,继而可得出结论;(3)过D作DM⊥BC,设AD=DM=MC=x,则可得DC=![]() x,根据AD+DC=AC=AB=5,可得关于x的方程,解出即可得出答案.
x,根据AD+DC=AC=AB=5,可得关于x的方程,解出即可得出答案.
本题解析:
证明:(1)△ABD≌△ACF.
∵AB=AC,∠BAC=90,
∴∠FAC=∠BAC=90,
∵BD⊥CE,∠BAC=90,
∴∠ADB=∠EDC,
∴∠ABD=∠ACF,
∵在△ABD和△ACF中,
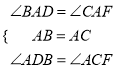 ,
,
∴△ABD≌△ACF(ASA),
(2)∵△ABD≌△ACF,
∴BD=CF,
∵BD⊥CE,
∴∠BEF=∠BEC,
∵BD是∠ABC的平分线,
∴∠FBE=∠CBE,
∵在△FBE和△CBE中,
 ,
,
∴△FBE≌△CBE(ASA),
∴EF=EC,
∴CF=2CE,
∴BD=2CE.
(3)过D作DM⊥BC,

∵AB=BM,设AD=DM=MC=x,
则 BC=MB+MC即5![]() =5+x
=5+x
解得:x=5![]() 5,
5,
则AD的长为5![]() 5.
5.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目