题目内容
 如图,OA,OB均为⊙O的半径,C为⊙O上一点,且∠OBA=55°,则∠ACB=
如图,OA,OB均为⊙O的半径,C为⊙O上一点,且∠OBA=55°,则∠ACB=
- A.30°
- B.35°
- C.60°
- D.70°
B
分析:根据等腰三角形性质得出∠OAB=∠OBA=55°,求出∠AOB,根据圆周角定理得出∠ACB= ∠AOB,代入即可.
∠AOB,代入即可.
解答:∵OA=OB,∠OBA=55°,
∴∠OAB=∠OBA=55°,
∴∠AOB=180°-55°-55°=70°,
∵弧AB对的圆心角是∠AOB,对的圆周角是∠ACB,
∴∠ACB= ∠AOB=35°,
∠AOB=35°,
故选B.
点评:本题考查了圆周角定理,等腰三角形的性质,三角形的内角和定理,注意:同圆或等圆中,圆周角等于它所对的弧上的圆心角的一半.
分析:根据等腰三角形性质得出∠OAB=∠OBA=55°,求出∠AOB,根据圆周角定理得出∠ACB=
 ∠AOB,代入即可.
∠AOB,代入即可.解答:∵OA=OB,∠OBA=55°,
∴∠OAB=∠OBA=55°,
∴∠AOB=180°-55°-55°=70°,
∵弧AB对的圆心角是∠AOB,对的圆周角是∠ACB,
∴∠ACB=
 ∠AOB=35°,
∠AOB=35°,故选B.
点评:本题考查了圆周角定理,等腰三角形的性质,三角形的内角和定理,注意:同圆或等圆中,圆周角等于它所对的弧上的圆心角的一半.

练习册系列答案
相关题目
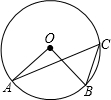 如图,已知OA,OB均为⊙O上一点,若∠AOB=80°,则∠ACB=( )
如图,已知OA,OB均为⊙O上一点,若∠AOB=80°,则∠ACB=( )| A、80° | B、70° | C、60° | D、40° |
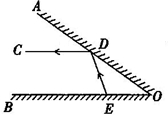 5、如图所示,∠AOB的两边.OA、OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,则∠DEB的度数是( )
5、如图所示,∠AOB的两边.OA、OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,则∠DEB的度数是( )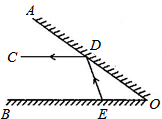 (2013•南安市质检)如图,∠AOB的两边OA、OB均为平面反光镜,∠AOB=40°,从OB上一点E射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,则∠DEB的度数是( )
(2013•南安市质检)如图,∠AOB的两边OA、OB均为平面反光镜,∠AOB=40°,从OB上一点E射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,则∠DEB的度数是( )