题目内容
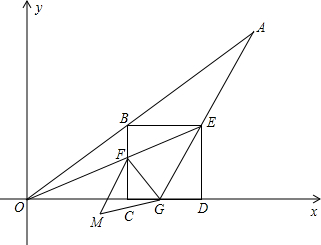
(2013•平阳县二模)在直角坐标系中,O为坐标原点,点A的坐标为(4,3),点B从点O出发以每秒一个单位的速度向点A运动,当点B到达A点时运动停止.过点B作BC⊥x轴,垂足为C,以BC为边在右侧作正方形BCDE.连接OE交BC于点F,连接AE并延长交x轴的正半轴于点G,连接FG.设点B的运动时间为t秒(t>0).
(1)直接写出正方形BCDE的边长:
t
t(用含t的代数式表示);
(2)用含t的代数式表示△OAG的面积S;
(3)当△OBE∽△OEA时(点E与点A对应,点O与点O对应),t的值是多少?,
(4)若M是点E关于直线FG的对称点,是否存在t的值,使得四边形EFMG是平行四边形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.
(1)直接写出正方形BCDE的边长:
| 3 |
| 5 |
| 3 |
| 5 |
(2)用含t的代数式表示△OAG的面积S;
(3)当△OBE∽△OEA时(点E与点A对应,点O与点O对应),t的值是多少?,
(4)若M是点E关于直线FG的对称点,是否存在t的值,使得四边形EFMG是平行四边形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.

分析:(1)利用A点坐标得出
=
,进而求出即可;
(2)利用BE∥OG,则△ABE∽△AOG,得出
=
,进而得出OG的长,即可得出答案;
(3)当△OBE∽△OEA时,则
=
,求出OE2=OB•OA=5t,进而利用勾股定理得出t的值;
(4)首先证明Rt△BEF≌Rt△DEG(HL),进而证明△FBE∽△EDO,则
=
,再利用DG=OD-OG或DG=OG-OD求出t的值.
| BC |
| BO |
| 3 |
| 5 |
(2)利用BE∥OG,则△ABE∽△AOG,得出
| BE |
| OG |
| AB |
| AO |
(3)当△OBE∽△OEA时,则
| OB |
| OE |
| OE |
| OA |
(4)首先证明Rt△BEF≌Rt△DEG(HL),进而证明△FBE∽△EDO,则
| BF |
| DE |
| BE |
| OD |
解答:解:(1)∵点A的坐标为(4,3),OB=t,
∴
=
,
∴BC=
t,
即正方形BCDE的边长:
t (用含t的代数式表示);
故答案为:
t;
(2)∵BE∥OG,
∴△ABE∽△AOG,
∴
=
,即
=
,
∴OG=
∴S△AOG=
×
×3=
;
(3)当△OBE∽△OEA时,
∴
=
,
∴OE2=OB•OA=5t,
∵Rt△ODE中,OE2=OD2+DE2=(
t+
t)2+(
t)2=
t2
∴5t=
t2,
∴t1=0(舍去),t2=
;
(4)∵M是点E关于直线FG的对称点,
∴EF=MF,EG=MG
若四边形EFMG是平行四边形,则平行四边形EFMG是菱形,EF=EG,
在 Rt△BEF和Rt△DEG中,
Rt△BEF和Rt△DEG中,
,
∴Rt△BEF≌Rt△DEG(HL),
∴DG=BF,
∵BE∥CO,
∴∠BEF=∠COE,
∵∠EBF=∠ODE,
∴△FBE∽△EDO,
∴
=
即
=
=
,
∴BF=
t=DG,
①如原图,DG=OD-OG=
t-
=
t,
∴解得:t=
②如备用图,DG=OG-OD=
-
t=
t,
∴解得:t=
.
∴
| BC |
| BO |
| 3 |
| 5 |
∴BC=
| 3 |
| 5 |
即正方形BCDE的边长:
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
(2)∵BE∥OG,
∴△ABE∽△AOG,
∴
| BE |
| OG |
| AB |
| AO |
| ||
| OG |
| 5-t |
| 5 |
∴OG=
| 3t |
| 5-t |
∴S△AOG=
| 1 |
| 2 |
| 3t |
| 5-t |
| 9t |
| 10-2t |
(3)当△OBE∽△OEA时,
∴
| OB |
| OE |
| OE |
| OA |
∴OE2=OB•OA=5t,
∵Rt△ODE中,OE2=OD2+DE2=(
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 58 |
| 25 |
∴5t=
| 58 |
| 25 |
∴t1=0(舍去),t2=
| 125 |
| 58 |
(4)∵M是点E关于直线FG的对称点,
∴EF=MF,EG=MG
若四边形EFMG是平行四边形,则平行四边形EFMG是菱形,EF=EG,
在
 Rt△BEF和Rt△DEG中,
Rt△BEF和Rt△DEG中,
|
∴Rt△BEF≌Rt△DEG(HL),
∴DG=BF,
∵BE∥CO,
∴∠BEF=∠COE,
∵∠EBF=∠ODE,
∴△FBE∽△EDO,
∴
| BF |
| DE |
| BE |
| OD |
| BF | ||
|
| ||
|
| 3 |
| 7 |
∴BF=
| 9 |
| 35 |
①如原图,DG=OD-OG=
| 7 |
| 5 |
| 3t |
| 5-t |
| 9 |
| 35 |
∴解得:t=
| 19 |
| 8 |
②如备用图,DG=OG-OD=
| 3t |
| 5-t |
| 7 |
| 5 |
| 9 |
| 35 |
∴解得:t=
| 185 |
| 58 |
点评:此题主要考查了相似形综合应用以及菱形的判定、勾股定理和相似三角形的判定与性质等知识,利用数形结合以及分类讨论得出是解题关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
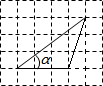 (2013•平阳县二模)三角形在方格纸中的位置如图所示,则cosα的值是( )
(2013•平阳县二模)三角形在方格纸中的位置如图所示,则cosα的值是( )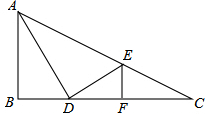 (2013•平阳县二模)如图,Rt△ABC中,∠B=90°,AD平分∠BAC,DE⊥AD交AC于点E,EF⊥BC于点F,若AB=4,BD=2,则CE的长为( )
(2013•平阳县二模)如图,Rt△ABC中,∠B=90°,AD平分∠BAC,DE⊥AD交AC于点E,EF⊥BC于点F,若AB=4,BD=2,则CE的长为( )