题目内容
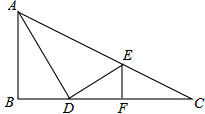 (2013•平阳县二模)如图,Rt△ABC中,∠B=90°,AD平分∠BAC,DE⊥AD交AC于点E,EF⊥BC于点F,若AB=4,BD=2,则CE的长为( )
(2013•平阳县二模)如图,Rt△ABC中,∠B=90°,AD平分∠BAC,DE⊥AD交AC于点E,EF⊥BC于点F,若AB=4,BD=2,则CE的长为( )分析:先利用勾股定理计算出AD=2
,再根据相似三角形的判定易得Rt△ABD∽Rt△ADE,运用相似比可计算出DE=
,AE=5;然后利用等角的余角相等得到∠ADB=∠DEF,于是可判断Rt△ADB∽Rt△DEF,运用相似比可计算出EF,接着由EF∥AB得到△CEF∽△CAB,再根据相似比可计算出CE.
| 5 |
| 5 |
解答:解:∵∠B=90°,AB=4,BD=2,
∴AD=
=2
,
∵AD平分∠BAC,
∴∠BAD=∠DAE,
∵DE⊥AD,
∴∠ADE=90°,
∴Rt△ABD∽Rt△ADE,
∴
=
=
,即
=
=
,
∴DE=
,AE=5,
∵EF⊥DF,
∴∠DFE=90°,
∴∠EDF+∠DEF=90°,
而∠ADB+∠EDF=90°,
∴∠ADB=∠DEF,
∴Rt△ADB∽Rt△DEF,
∴
=
,即
=
,解得EF=1,
∵EF∥AB,
∴△CEF∽△CAB,
∴
=
,即
=
,
∴CE=
.
故选B.
∴AD=
| AB2+BD2 |
| 5 |
∵AD平分∠BAC,
∴∠BAD=∠DAE,
∵DE⊥AD,
∴∠ADE=90°,
∴Rt△ABD∽Rt△ADE,
∴
| AB |
| AD |
| BD |
| DE |
| AD |
| AE |
| 4 | ||
2
|
| 2 |
| DE |
2
| ||
| AE |
∴DE=
| 5 |
∵EF⊥DF,
∴∠DFE=90°,
∴∠EDF+∠DEF=90°,
而∠ADB+∠EDF=90°,
∴∠ADB=∠DEF,
∴Rt△ADB∽Rt△DEF,
∴
| BD |
| EF |
| AD |
| DE |
| 2 |
| EF |
2
| ||
|
∵EF∥AB,
∴△CEF∽△CAB,
∴
| CE |
| CA |
| EF |
| AB |
| CE |
| CE+5 |
| 1 |
| 4 |
∴CE=
| 5 |
| 3 |
故选B.
点评:本题考查了相似三角形的判定与性质:有两组角对应相等的两个三角形相似;相似三角形的对应边的比相等.也考查了勾股定理.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
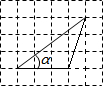 (2013•平阳县二模)三角形在方格纸中的位置如图所示,则cosα的值是( )
(2013•平阳县二模)三角形在方格纸中的位置如图所示,则cosα的值是( )