Question

【题目】如图，已知⊙O为△ABC的外接圆，BC为直径，点E在AB上，过点E作EF⊥BC，点G在FE的延长线上，且GA＝GE.

(1) 求证：AG与⊙O相切；

(2)若AC＝5，AB＝12，BE＝，求线段OE的长．

Answer 1

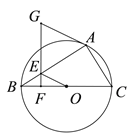
【答案】（1）证明见解析；

（2）OE的长为.

【解析】解：(1) 证明：如图

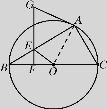
连接OA，∵OA＝OB，GA＝GE，

∴∠ABO＝∠BAO，∠GEA＝∠GAE.

∵EF⊥BC，∴∠BFE＝90°，∴∠ABO＋∠BEF＝90°.

又∵∠BEF＝∠GEA，∴∠GAE＝∠BEF. ……………2分

∴∠BAO＋∠GAE＝90°，∴OA⊥AG，即AG与⊙O相切

(2)解：∵BC为直径，∴∠BAC＝90°，∵AC＝5，AB＝12，∴BC＝13.

∵∠EBF＝∠CBA，∠BFE＝∠BAC， ∴△BEF∽△BCA.

∴＝＝，∴EF＝ ，BF＝4，

∴OF＝OB－BF＝－ 4＝ . ∴OE＝＝.