题目内容
【题目】材料一：一个正整数x能写成x=a2﹣b2（a，b均为正整数，且a≠b），则称x为“雪松数”，a，b为x的一个平方差分解，在x的所有平方差分解中，若a2+b2最大，则称a，b为x的最佳平方差分解，此时F（x）=a2+b2．
例如：24=72﹣52，24为雪松数，7和5为24的一个平方差分解，32=92﹣72，32=62﹣22，因为92+72＞62+22，所以9和7为32的最佳平方差分解，F（32）=92+72
材料二：若一个四位正整数，它的千位数字与个位数字相同，百位数字与十位数字相同，但四个数字不全相同，则称这个四位数为“南麓数”．例如4334，5665均为“南麓数”．
根据材料回答：
（1）请直接写出两个雪松数，并分别写出它们的一对平方差分解；
（2）试证明10不是雪松数；
（3）若一个数t既是“雪松数”又是“南麓数”，并且另一个“南麓数”的前两位数字组成的两位数与后两位数字组成的两位数恰好是t的一个平方差分解，请求出所有满足条件的数t中F（t）的最大值．
【答案】（1）112=112﹣32，40=72﹣32；（2）见解析；（3）12020．
【解析】试题分析：（1）根据雪松数的特征即可得到结论；
（2）根据题意即可得到结论；
（3）设t=
（a，b均为正整数，且0＜a≠b≤9），另一个“南麓数”为t′=
（m，n均为正整数，且0＜n＜m≤9），根据“南麓数”的特征即可得到结论．
试题解析：解：（1）112=112﹣32，40=72﹣32；
（2）若10是“雪松数”，则可设a2﹣b2=10（a，b均为正整数，且a≠b），则（a+b）（a﹣b）=10．又∵10=2×5=10×1．∵a，b均为正整数，∴a+b＞a﹣b，∴
，或
，解得：
或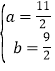
，与a，b均为正整数矛盾，故10不是雪松数；
（3）设t=（a，b均为正整数，且0＜a≠b≤9），另一个“南麓数”为t′=（m，n均为正整数，且0＜n＜m≤9），则t=（10m+n）2﹣（10n+m）2=99（m2﹣n2）=99（m+n）（m﹣n），∴99（m+n）（m﹣n）=1000a+100b+10b+a=1001a+110b，整理得，（m+n）（m﹣n）=10a+b+
．∵a，b，m，n均为正整数，∴a+b=9，经探究
，符合题意，∴t的值分别为：2772，5445，t′的值分别为：8668，8338，由材料一可知，F（t）的最大值为：862+682=12020．
