Question

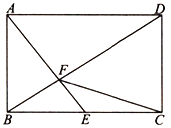
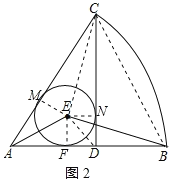
【题目】如图，在扇形CAB中，CD⊥AB，垂足为D，圆E是△ACD的内切圆，切点分别为M，N，F，连接AE，BE.

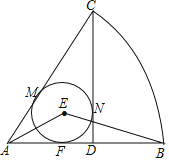
（1）求∠AEB的度数；

（2）若AD＝DB，CD＝3，求扇形CAB的弧长和圆E的半径．

Answer 1

【答案】（1）∠AEB＝135°；（2）扇形CAB的弧长为，圆E的半径为．

【解析】

（1）连接EC．首先求出∠AEC=135°，再证明△EAC≌△EAB即可解决问题；

（2）连接BC、EF、EM、EN、DE，证明△ABC是等边三角形，得出∠BAC=60°，由直角三角形的性质得出ADCD，得出AB=AC=2，由弧长公式求出扇形CAB的弧长，由切线的性质和三角形面积可求出圆E的半径．

（1）连接EC．如图1所示：

∵E是△ADC的内心，∠ADC=90°，∴∠ACE∠ACD，∠EAC∠CAD，∴∠AEC=180°（∠ACD+∠CAD）=135°，

在△AEC和△AEB中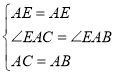，∵，∴△EAC≌△EAB（SAS），∴∠AEB=∠AEC=135°；

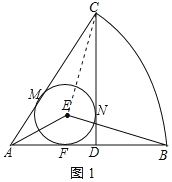
（2）连接BC、EF、EM、EN、DE，如图2所示：

∵CD⊥AB，AD=DB，∴AC=BC．

∵AC=AB，∴AB=AC=BC，∴△ABC是等边三角形，∴∠BAC=60°，∴∠ACD=30°，∴ADCD，∴AB=AC=2，∴扇形CAB的弧长为，

∵圆E是△ACD的内切圆，切点分别为M，N，F，∴EF⊥AD，EN⊥CD，EM⊥AC，EM=EF=EN．

∵CD⊥AB，∴△ACD的面积=△ACE的面积+△ADE的面积+△CDE的面积，

即32EMEF3×EN，

解得：EF，

即圆E的半径为．