题目内容
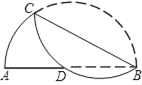
【题目】将![]() 沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( )
沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( )
A. 3![]() B. 8 C.
B. 8 C. ![]() D. 2
D. 2![]()
【答案】A
【解析】
若连接CD、AC,则根据同圆或等圆中,相等的圆周角所对的弦相等,求得AC=CD;过C作AB的垂线,设垂足为E,则DE=![]() AD,由此可求出BE的长,进而可在Rt△ABC中,根据射影定理求出BC的长.
AD,由此可求出BE的长,进而可在Rt△ABC中,根据射影定理求出BC的长.

连接CA、CD,
根据折叠的性质,知弧CD所对的圆周角等于∠CBD,
又∵弧AC所对的圆周角是∠CBA,
∵∠CBD=∠CBA,
∴AC=CD(相等的圆周角所对的弦相等) ,
∴△CAD是等腰三角形,
过C作CE⊥AB于E.
∵AD=4,则AE=DE=2,
∴BE=BD+DE=7,
在Rt△ACB中,CE⊥AB,根据射影定理,得:
![]() =BEAB=7×9=63,
=BEAB=7×9=63,
故BC=![]() .
.
故选:A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目