题目内容
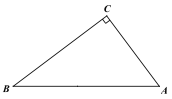
【题目】如图，Rt△ABC，AC⊥CB,AC=15，AB=25,点D为斜边上动点。
（1）如图，过点D作DE⊥AB交CB于点E,连接AE,当AE平分∠CAB时，求CE；
（2）如图，在点D的运动过程中，连接CD，若△ACD为等腰三角形，求AD。
【答案】（1）7.5（2）①15②12.5③18
【解析】
（1）在Rt△ABC中， AC=15，AB=25，由勾股定理得BC=20，根据角平分线的性质得DE=DC，证得△ACE≌△AED，AD=AC=15， BD=25-15=10，设CE=x,则BE=20-x，在在Rt△BED中，由勾股定理得
，解得x=7.5，即CE=7.5.（2）若△ACD为等腰三角形，分三种情况，即CD=AC、CD=AD或AD=AC，利用等腰三角形的三线合一性质和三角形面积即可解答，难度不大.
(1) ∵AC⊥CB,AC=15，AB=25
∴BC=20
∵AE平分∠CAB
∴∠EAC=∠EAD
∵AC⊥CB, DE⊥AB
∴∠EDA=∠ECA=90°
∵AE=AE
∴△ACE≌△AED
∴CE=DE,AC=AD=15
设CE=x,则BE=20-x,BD=25-15=10
在Rt△BED中
∴
∴x=7.5
∴CE=7.5
(2) ①当AD=AC时，△ACD为等腰三角形
∵AC=15 ∴AD=AC=15
②当CD=AD时，△ACD为等腰三角形
∵CD=AD
∴∠DCA=∠CAD
∵∠CAB+∠B=90°
∠DCA+∠BCD=90°
∴∠B=∠BCD
∴BD=CD
∴CD=BD=DA=12.5
③当CD=AC时，△ACD为等腰三角形
如图，作CH⊥BA于点H,
则
∵AC=15，BC=20，AB=25
∴CH=12
在Rt△ACH中，易求AH=9
∵CD=AC , CH⊥BA
∴DH=HA=9
∴AD=18
