题目内容
【题目】如图,已知二次函数y=a(x﹣h)2+![]() 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).
写出该函数图象的对称轴;

【答案】对称轴为直线x=1
【解析】试题分析:
本题要求二次函数的对称轴. 分析题目条件可知本题可以用两种方法解决. 其一,因为已知的两个点均为二次函数与x轴的交点,所以点O与点A必定关于二次函数的对称轴对称. 根据对称性可知,该二次函数的对称轴与x轴的交点必定是线段OA的中点. 利用该几何性质容易得到该二次函数的对称轴. 其二,由于点O与点A均在二次函数的图象上,所以点O与点A的坐标一定满足该二次函数的解析式. 将这两点的坐标代入解析式并联立,即可得到一个方程组,解之可得a与h的值. 这样就确定了该二次函数的解析式,进而可以获得二次函数的对称轴.
试题解析:
(解法一)
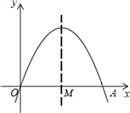
如图,设该二次函数的对称轴与x轴的交点为M.
∵点O与点A均为该二次函数与x轴的交点,
∴点O与点A关于该二次函数的对称轴对称,
∴在x轴上,线段OA的中点为点M,即![]() ,
,
∵点O的坐标为(0, 0),点A的坐标为(2, 0),
∴OA=2,
∴![]() ,
,
∴点M的坐标为(1, 0),
∵点M为该二次函数的对称轴与x轴的交点,
∴该二次函数的对称轴为直线x=1.
(解法二)
∵二次函数![]() 的图象经过点O(0, 0)与点A(2, 0),
的图象经过点O(0, 0)与点A(2, 0),
∴将点O与点A的坐标代入二次函数解析式,得
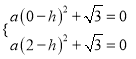 ,
,
解这个方程组:
 ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,①
,①
∵在二次函数![]() 中,a≠0,
中,a≠0,
∴①式两侧同时除以a,得 h=1.
∴![]() .
.
∴该二次函数的解析式为![]() .
.
∴该二次函数的对称轴为直线x=1.

练习册系列答案
相关题目