��Ŀ����
��ͼ����֪����ABCD�У�AD��BC��AB��BC��AB=4��AD=CD=5��cot��C=| 3 | 4 |
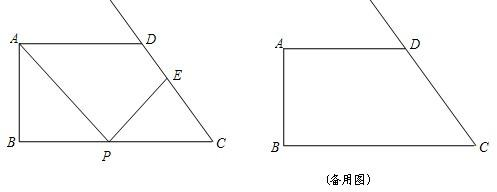
��1����PE=CEʱ����BP�ij��ȣ�
��2������E�����߶�CD��ʱ����BP=x��DE=y������y��x֮��ĺ�����ϵ����д���䶨����
��3������PD�����Ե�A��P��DΪ��������������PCE���ƣ�����BP�ij��ȣ�
��������1���ȸ�����֪֤����APB=��C���ٸ������Ǻ�����֪ʶ�ó�PE=CEʱ��BP�ij��ȣ�
��2���ӳ�PE��AD���ӳ��߽��ڵ�F������ƽ���ߵ����ʼ��ɵó���x֮��ĺ�����ϵ��
��3������APD���PCE���ƣ����������������������ADP=��Cʱ����APD�ס�PEC���������������ε����ʵó�BP�ij��ȣ���������APD=��Cʱ����APD�ס�DCP���������������ε����ʵó�BP�ij��ȣ�
��2���ӳ�PE��AD���ӳ��߽��ڵ�F������ƽ���ߵ����ʼ��ɵó���x֮��ĺ�����ϵ��
��3������APD���PCE���ƣ����������������������ADP=��Cʱ����APD�ס�PEC���������������ε����ʵó�BP�ij��ȣ���������APD=��Cʱ����APD�ס�DCP���������������ε����ʵó�BP�ij��ȣ�
���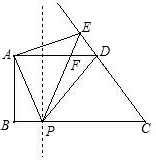 �⣺��1��������֪����BC=8����APB=��EPC��1�֣�
�⣺��1��������֪����BC=8����APB=��EPC��1�֣�
��PE=CE���EPC=��C
���APB=��C
������һ����cot��C=
��
=
��1�֣�
��AB=4��BP=3��1�֣�
��BP=3ʱ��PE=CE
������������AP��DC
��PC=AD=5��1�֣�
��BP=3��1�֣�
��BP=3ʱ��PE=CE
��2���ӳ�PE��AD���ӳ��߽��ڵ�F��
��BP=x��
�߹��ߴӵ�A��������AP�ķ����������BC���䣬
��PC=8-x��AF=2x��1�֣�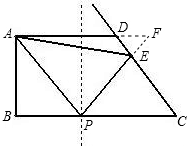
��DE=y��DC=AD=5��
��EC=5-y��DF=2x-5
��AF��BC
��
=
��1�֣�
��
=
��1�֣�
��y=
��1�֣�
�ߵ�E���߶�CD��
�ຯ��������Ϊ
��x��8��1�֣�
��3����AD��BC���DAP=��APB��
�ߡ�APB=��EPC���DAP=��EPC��1�֣�
����APD���PCE���ƣ������������������
��������ADP=��Cʱ��
�Ƴ�BP=2ʱ����APD�ס�PEC����2�֣�
��������APD=��Cʱ
����һ���֡ߡ�ADP=��DPC���APD�ס�DCP
��PD2=AD•PC
��PD2=42+��5-x��2��1�֣�
��16+��5-x��2=5��8-x����1�֣�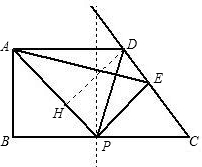
���x1��2=
�������飬����������
��x1��2=
ʱ����APD�ס�PCE����1�֣�
�൱BPΪ2��
ʱ����APD���PCE���ƣ�
������������D��DH��AP�ڵ�H
�ߡ�DAP=��APB��
=
��
=
��AP=
��DH=
��AH=
��HP=
-
��1�֣�
��cot��C=
��
4(
-
)=3•
��1�֣�
���x=
����x=
��
��x=
ʱ����APD�ס�PCE����1�֣�
�൱BPΪ2��
ʱ����APD���PCE���ƣ�
 �⣺��1��������֪����BC=8����APB=��EPC��1�֣�
�⣺��1��������֪����BC=8����APB=��EPC��1�֣���PE=CE���EPC=��C
���APB=��C
������һ����cot��C=
| 3 |
| 4 |
| BP |
| AB |
| 3 |
| 4 |
��AB=4��BP=3��1�֣�
��BP=3ʱ��PE=CE
������������AP��DC
��PC=AD=5��1�֣�
��BP=3��1�֣�
��BP=3ʱ��PE=CE
��2���ӳ�PE��AD���ӳ��߽��ڵ�F��
��BP=x��
�߹��ߴӵ�A��������AP�ķ����������BC���䣬
��PC=8-x��AF=2x��1�֣�

��DE=y��DC=AD=5��
��EC=5-y��DF=2x-5
��AF��BC
��
| DF |
| PC |
| DE |
| EC |
��
| 2x-5 |
| 8-x |
| y |
| 5-y |
��y=
| 5(2x-5) |
| x+3 |
�ߵ�E���߶�CD��
�ຯ��������Ϊ
| 5 |
| 2 |
��3����AD��BC���DAP=��APB��
�ߡ�APB=��EPC���DAP=��EPC��1�֣�
����APD���PCE���ƣ������������������
��������ADP=��Cʱ��
�Ƴ�BP=2ʱ����APD�ס�PEC����2�֣�
��������APD=��Cʱ
����һ���֡ߡ�ADP=��DPC���APD�ס�DCP
��PD2=AD•PC
��PD2=42+��5-x��2��1�֣�
��16+��5-x��2=5��8-x����1�֣�

���x1��2=
5��
| ||
| 2 |
��x1��2=
5��
| ||
| 2 |
�൱BPΪ2��
5��
| ||
| 2 |
������������D��DH��AP�ڵ�H
�ߡ�DAP=��APB��
| AB |
| AP |
| DH |
| AD |
| BP |
| AP |
| AH |
| AD |
��AP=
| 42+x2 |
��DH=
| 20 | ||
|
| 5x | ||
|
��HP=
| 16+x2 |
| 5x | ||
|
��cot��C=
| a |
| b |
| 16+x2 |
| 5x | ||
|
| 20 | ||
|
���x=
5+
| ||
| 2 |
5-
| ||
| 2 |
��x=
5��
| ||
| 2 |
�൱BPΪ2��
5��
| ||
| 2 |
������������Ҫ���������ε����ʣ�ƽ���ߵ����ʣ����������ε��ж��������Լ�����֪ʶ���ۺ�Ӧ�ã�Ҫ���ݶ�Ӧ�ǵIJ�ͬ���з�����⣮

��ϰ��ϵ�д�
 ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
�����Ŀ
 9����ͼ����֪����ABCD�У�AD��BC��BEƽ�֡�ABC��BE��CD����A=110�㣬AD=3��AB=5����BC�ij�Ϊ��������
9����ͼ����֪����ABCD�У�AD��BC��BEƽ�֡�ABC��BE��CD����A=110�㣬AD=3��AB=5����BC�ij�Ϊ��������
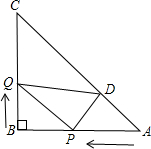 �㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ����Q��QD��AB��AC�ڵ�D������PD�����˶�ʱ��Ϊt��ʱ���ı���BQDP�����Ϊs��
�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ����Q��QD��AB��AC�ڵ�D������PD�����˶�ʱ��Ϊt��ʱ���ı���BQDP�����Ϊs�� ��2007•��������ͼ����֪������ABC�����Ϊ4cm2����D��E�ֱ���AB��AC�ߵ��е㣬������DBCE�����Ϊ
��2007•��������ͼ����֪������ABC�����Ϊ4cm2����D��E�ֱ���AB��AC�ߵ��е㣬������DBCE�����Ϊ