题目内容
已知整数k<5,若△ABC的边长均满足关于x的方程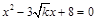 ,则△ABC的周长是 .
,则△ABC的周长是 .
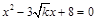 ,则△ABC的周长是 .
,则△ABC的周长是 .6或12或10.
试题分析:根据题意得k≥0且(
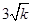 )2-4×8≥0,而整数k<5,则k=4,方程变形为x2-6x+8=0,解得x1=2,x2=4,由于△ABC的边长均满足关于x的方程x2-6x+8=0,
)2-4×8≥0,而整数k<5,则k=4,方程变形为x2-6x+8=0,解得x1=2,x2=4,由于△ABC的边长均满足关于x的方程x2-6x+8=0,所以△ABC的边长可以为2、2、2或4、4、4或4、4、2,然后分别计算三角形周长.
试题解析:根据题意得k≥0且(
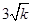 )2-4×8≥0,
)2-4×8≥0,解得k≥
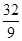 ,
,∵整数k<5,
∴k=4,
∴方程变形为x2-6x+8=0,解得x1=2,x2=4,
∵△ABC的边长均满足关于x的方程x2-6x+8=0,
∴△ABC的边长为2、2、2或4、4、4或4、4、2,
∴△ABC的周长为6或12或10.
故答案为:6或12或10.
考点: 1.根的判别式;2.解一元二次方程-因式分解法;3.三角形三边关系.

练习册系列答案
相关题目
 x﹣4=0.
x﹣4=0.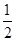 )-1-cos45°+3×(2012-π)0 ⑵解方程:2x2-4x+1=0 (配方法)
)-1-cos45°+3×(2012-π)0 ⑵解方程:2x2-4x+1=0 (配方法) 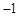
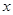 的一元二次方程
的一元二次方程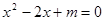 有两个不相等的实数根,则
有两个不相等的实数根,则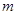 的取值范围是( )。
的取值范围是( )。



 ,已知第二块木板的面积比第一块大
,已知第二块木板的面积比第一块大 ,这两块木板的长和宽分别是( )
,这两块木板的长和宽分别是( ) ,宽
,宽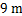 ,第二块木板长
,第二块木板长 ,宽
,宽
 ,宽
,宽 ,第二块木板长
,第二块木板长
 ,第二块木板长
,第二块木板长 ,宽
,宽
 满足
满足 _____.
_____.