题目内容
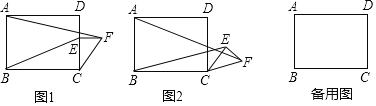
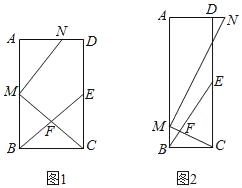
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连接CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)如图1,当点F为BE中点时,求证:AM=CE;
(2)如图2,若![]() =3时,求
=3时,求![]() 的值;
的值;
(3)若![]() =n(n≥3)时,请直接写出
=n(n≥3)时,请直接写出![]() 的值.(用含n的代数式表示)
的值.(用含n的代数式表示)
【答案】(1)见解析;(2)5;(3)![]()
【解析】
(1)由F为BE的中点,可得BF=EF,因为四边形ABCD为矩形,可得∠BCE=∠ABC=90°,CF=BF=EF,∠FBC=∠FCB,可推出△MBC≌△ECB,则可推导出AM=CE.
(2)根据AB∥CD,可得![]() =3,设MB=a,则EC=DE=3a,AB=CD=6a,根据
=3,设MB=a,则EC=DE=3a,AB=CD=6a,根据![]() =3,可得BC=AD=2a,根据MN⊥CM,可推出△AMN∽△BCM,则可得
=3,可得BC=AD=2a,根据MN⊥CM,可推出△AMN∽△BCM,则可得![]() ,
,![]() ,推出AN=
,推出AN=![]() ,DN=
,DN=![]() a,则
a,则![]() =5.
=5.
(3)同(2)的推导方法.
解:(1)∵F为BE的中点,
∴BF=EF,
∵四边形ABCD为矩形,
∴∠BCE=∠ABC=90°,
∴CF=BF=EF,
∴∠FBC=∠FCB,
∵BC=CB,
∴△MBC≌△ECB(AAS),
∴BM=EC=DE,
∵AB=CD,
∴BM=AM,
∴AM=CE.
(2)∵AB∥CD,
∴![]() =3,
=3,
设MB=a,则EC=DE=3a,
∴AB=CD=6a,
∵![]() =3,
=3,
∴BC=AD=2a,
∵MN⊥CM,
∴△AMN∽△BCM,
∴![]() ,
,
∴![]() ,
,
∴AN=![]() ,
,
DN=![]() a,
a,
∴![]() =5.
=5.
(3)∵AB∥CD,
∴![]() =n,
=n,
设MB=a,则EC=DE=an,
∴AB=CD=2an,
∵![]() =n,
=n,
∴BC=AD=2a,
∵MN⊥CM,
∴△AMN∽△BCM,
∴![]() ,
,
∴![]() ,
,
∴AN=![]() ,
,
DN=![]()
∴![]() .
.

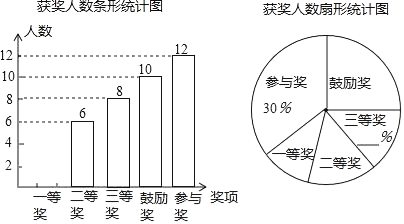
【题目】某校为了解九年级全体学生物理实验操作的情况,随机抽取了30名学生的物理实验操作考核成绩,并将数据进行整理,分析如下: (说明:考核成绩均取整数,A级:10分,B级:9分,C级:8分,D级:7分及以下)
收集数据
10,8,10,9,5,10,9,9,10,8,9,10,9,9,8,9,8,10,7,9,8,10,9,6,9,10,9,10,8,10
整理数据
整理、描述样本数据,绘制统计表如下:
抽取的30名学生物理实验操作考核成绩频数统计表
成绩等级 | A | B | C | D |
人数(名) | 10 | m | n | 3 |
根据表中的信息,解答下列问题:
(1)m=________,n=________;
(2)若该校九年级共有800名学生参加物理实验操作考核,成绩不低于9分为优秀,试估计该校九年级参加物理实验操作考核成绩达到优秀的学生有多少名?
(3)甲、乙、丙、丁是九年级1班物理实验考核成绩为10分的四名学生,学校计划从这四名学生中随机选出两名学生代表学校去参加全市中学生“物理实验操作”竞赛,用列表法或画树状图法,求甲、乙两名学生中至少有一名被选中的概率.