Question

如图，平行四边形ABCD中，AB＝5，BC＝10，BC边上的高AM＝4，E为BC边上的一个动点(不与B、C重合)．过E作直线AB的垂线，垂足为F．FE与DC的延长线相交于点G，连结DE，DF．

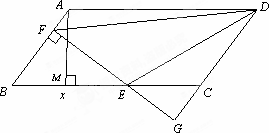
(1)求证：ΔBEF∽ΔCEG．

(2)当点E在线段BC上运动时，△BEF和△CEG的周长之间有什么关系？并说明你的理由．

(3)设BE＝x，△DEF的面积为y，请你求出y和x之间的函数关系式，并求出当x为何值时，y有最大值，最大值是多少？

Answer 1

答案：
解析：

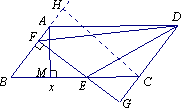
(1)因为四边形ABCD是平行四边形，所以　　1分 　　所以 　　所以　　3分 　　(2)的周长之和为定值　　4分 　　理由一： 　　过点C作FG的平行线交直线AB于H， 　　因为GF⊥AB，所以四边形FHCG为矩形．所以FH＝CG，FG＝CH 　　因此，的周长之和等于BC＋CH＋BH 　　由BC＝10，AB＝5，AM＝4，可得CH＝8，BH＝6， 　　所以BC＋CH＋BH＝24　　6分 　　理由二： 　　由AB＝5，AM＝4，可知 　　在Rt△BEF与Rt△GCE中，有： 　　， 　　所以，△BEF的周长是，△ECG的周长是 　　又BE＋CE＝10，因此的周长之和是24　　6分 　　(3)设BE＝x，则 　　所以　　8分 　　配方得：． 　　所以，当时，y有最大值　　10分 　　最大值为　　12分