题目内容
已知抛物线y=ax2+3ax+b交x轴分别于A、B(1,0),交y轴于C(0,2).(1)求此抛物线的解析式;
(2)如图(1),P为抛物线第三象限的点,若S△PAC=2S△PBC,求P点坐标;
(3)如图(2),D为抛物线的顶点,在抛物线上是否存在点Q,使△ADQ为锐角三角形?若存在,求出Q点横坐标的取值范围.
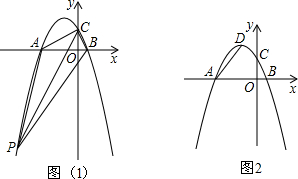
分析:(1)将B、C两点坐标代入抛物线解析式,可求a、b的值,确定抛物线解析式;
(2)设PC交线段AB于M点,只需要AM=2MB即可,根据A、B两点坐标求M点坐标,再求直线CM,与抛物线解析式联立,可求P点坐标;
(3)根据∠ADQ=90°,∠DAQ=90°分别求Q点的横坐标,得出△ADQ为锐角三角形时,Q点横坐标的取值范围.
(2)设PC交线段AB于M点,只需要AM=2MB即可,根据A、B两点坐标求M点坐标,再求直线CM,与抛物线解析式联立,可求P点坐标;
(3)根据∠ADQ=90°,∠DAQ=90°分别求Q点的横坐标,得出△ADQ为锐角三角形时,Q点横坐标的取值范围.
解答:解:(1)把B(1,0),C(0,2)代入y=ax2+3ax+b中,得
,
解得
,
∴y=-
x2-
x+2;
(2)设PC交x轴于M,由(1)可知,A(-4,0),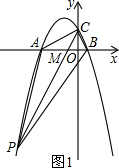
∴AB=5,
若S△PAC=2S△PBC,
则AM=2MB=
AB=
,M点横坐标为-(4-AM)=-
,
∴直线CM:y=3x+2,联立
得P(-9,-25);
(3)连接CD,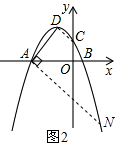
∵A(-4,0),D(-
,
),
∴直线AD:y=
x+5,
过A作AD的垂线,交抛物线于N点,
则直线AN:y=-
x-
,联立
,
解得N(
,-
),
同理,过D作AD的垂线,得N′(
,
),
∴
<xQ<
.
|
解得
|
∴y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)设PC交x轴于M,由(1)可知,A(-4,0),

∴AB=5,
若S△PAC=2S△PBC,
则AM=2MB=
| 2 |
| 3 |
| 10 |
| 3 |
| 2 |
| 3 |
∴直线CM:y=3x+2,联立
|
得P(-9,-25);
(3)连接CD,

∵A(-4,0),D(-
| 3 |
| 2 |
| 25 |
| 8 |
∴直线AD:y=
| 5 |
| 4 |
过A作AD的垂线,交抛物线于N点,
则直线AN:y=-
| 4 |
| 5 |
| 16 |
| 5 |
|
解得N(
| 13 |
| 5 |
| 132 |
| 25 |
同理,过D作AD的垂线,得N′(
| 1 |
| 10 |
| 1917 |
| 100 |
∴
| 1 |
| 10 |
| 13 |
| 5 |
点评:本题考查了二次函数的综合运用.关键是根据题意求抛物线解析式,根据直线解析式和抛物线解析式求交点坐标.

练习册系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=