Question

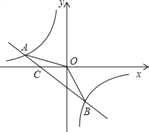
【题目】如图，在直角坐标系中，以点为圆心，以为半径的圆与轴相交于点，与轴相交于点．

（1）若抛物线经过两点，求抛物线的解析式，并判断点是否在该抛物线上．

（2）在（1）中的抛物线的对称轴上求一点，使得的周长最小．

（3）设为（1）中的抛物线的对称轴上的一点，在抛物线上是否存在这样的点，使得四边形是平行四边形．若存在，求出点的坐标；若不存在，说明理由．

Answer 1

【答案】(1) ;(2)见解析;(3)存在，理由见解析.

【解析】

试题（1）由已知条件先求出C，D两点的坐标，再把其横纵坐标分别代入抛物线的解析式求出b，c，再将点B坐标代入检验即可；（2）BD的长为定值，所以要使△PBD周长最小，只需PB+PD最小，连接DC，则DC与对称轴的交点即为使△PBD周长最小的点；（3）设Q（，t）为抛物线对称轴x=

上一点，M在抛物线上，要使四边形BCQM为平行四边形，则BC∥QM且BC=QM，再分①当点M在对称轴的左侧时和①当点M在对称轴的右侧时，讨论即可.

试题解析：（1）∵OA=，AD=AC=2，∴C（3，0），B（，0）.

又在Rt△AOD中，OA=，∴OD=. ∴D.

又∵D，C两点在抛物线上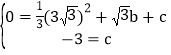，∴，解得.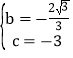

∴抛物线的解析式为.

又∵当时，，

∴点B（，0）在该抛物线上.

（2）∵，∴抛物线的对称轴方程为：x=.

∵BD的长为定值，∴要使△PBD周长最小，只需PB+PD最小.

连接DC，则DC与对称轴的交点即为使△FBD周长最小的点，

设直线DC的解析式为y=mx+n，，解得.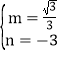

∴直线DC的解析式为.

在中令x=得y=. ∴P的坐标为.

（3）存在，

设Q（，t）为抛物线对称轴x=上一点，M在抛物线上，

要使四边形BCQM为平行四边形，则BC∥QM且BC=QM，且点M在对称轴的左侧，

过点Q作直线L∥BC与抛物线交于点M（x，t），由BC=QM得QM=4，从而x=，t=12.

故在抛物线上存在点M（，12）使得四边形BCQM为平行四边形.