题目内容
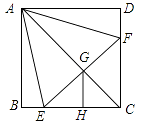
【题目】如图,正方形ABCD中.点E,F分别在BC,CD上,△AEF是等边三角形.连接AC交EF于点G.过点G作GH⊥CE于点H.若 ![]() ,则
,则 ![]() =( )
=( )
A.6
B.4
C.3
D.2
【答案】A
【解析】∵四边形ABCD是正方形,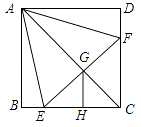
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°,
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
∵AE=AF,AB=AD,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=CD,
∴BC﹣BE=CD﹣DF,即CE=CF,
∴△CEF是等腰直角三角形,
∵AE=AF,
∴AC垂直平分EF,
∴EG=GF,
∵GH⊥CE,
∴GH∥CF,
∴△EGH∽△EFC,
∵S△EGH=3,
∴S△EFC=12,
∴CF= ![]() ,EF=
,EF= ![]() ,
,
∴AF= ![]() ,设AD=x,则DF=x﹣
,设AD=x,则DF=x﹣ ![]() ,
,
∵AF2=AD2+DF2 ,
∴( ![]() )2=x2+(x﹣
)2=x2+(x﹣ ![]() )2 ,
)2 ,
∴x= ![]() ,
,
∴AD= ![]() ,DF=
,DF= ![]() ,
,
∴S△ADF= ![]() ADDF=6.
ADDF=6.
故答案为:A.
根据正方形的性质及等边三角形的性质易证明AE=AF,AB=AD,根据直角三角形全等判定证明Rt△ABE≌Rt△ADF,得出BE=DF,从而证得CE=CF,得出△CEF是等腰直角三角形,再证明GH∥CF,得出△EGH∽△EFC,根据相似三角形的性质及S△EGH=3,求出△EFC的面积,从而求出AF和CE的长,然后设AD=x,利用勾股定理求出AD的长及DF的长,根据三角形的面积公式即可得出答案。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目