Question

【题目】如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，BC＝6，点D是BC边上一动点（不与B、C重合），过点D作DE⊥BC交AB边于点E，将∠B沿直线DE翻折，点B落在射线BC上的点F处，当△AEF为直角三角形时，BD的长为_____．

Answer 1

【答案】2或4

【解析】

分两种情况来解：

（1）当∠AFE=90°时，在Rt△ABC中，根据特殊锐角三角函数值可求得AB＝，然后由翻折的性质可求得∠AEF=60°，从而可求得∠EAF=30°，故此AE=2EF，由翻折的性质可知:BE=EF，故此AB=3BE，所以EB=，最后在Rt△BED中利用特殊锐角三角函数值即可求得BD的长；

（2）当点F在BC的延长线上时，∠EAF=90°，然后依据角平分线的性质可得到ED=AE，然后再证明△BED∞△BAC，最后依据相似三角形的性质求解即可．

解：分两种情况：

（1）当∠AFE=90°时，如解图1所示

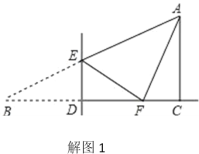∵Rt△ABC中，∠ACB＝90°，∠B＝30°，

∴，即．

∴AB＝

∵∠B＝30°，DE⊥BC，

∴∠BED＝60°．

由翻折的性质可知：∠BED＝∠FED＝60°，

∴∠AEF＝60°．

∵△AEF为直角三角形，

∴∠EAF＝30°．

∴AE＝2EF．

由翻折的性质可知：BE＝EF，

∴AB＝3BE．

∴EB＝．

在Rt△BED中，∠B＝30°，

∴，即．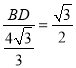

∴BD＝2．

（2）当∠EAF=90°时,点F在BC的延长线上．如解图2所示：

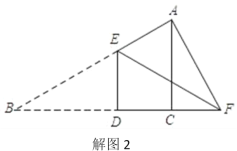∵△AEF为直角三角形，

∴∠EAF＝90°，

∴∠EFA＝30°．

∴∠EFD＝∠EFA．

又∵ED⊥BF，EA⊥AF，

∴AE＝DE．

∵BC＝6，∠ACB＝90°，∠B＝30°，

∴AB＝，AC＝

设DE＝x，BE＝﹣x．

∵DE∥AC，

∴，，解得：x＝．

∴BD＝DE＝×=4

故答案为：2或4．