Question

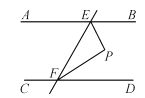
【题目】如图，AB∥CD，直线EF分别交AB，CD于点E，F，∠BEF的平分线与∠DFE的平分线相交于点P，试说明△EPF为直角三角形.

Answer 1

【答案】证明见解析

【解析】试题分析：由AB∥CD，可知∠BEF与∠DFE互补，由角平分线的性质可得∠PEF+∠PFE=90°，由三角形内角和定理可得∠P=90°，即可判定△EPF为直角三角形.．

试题解析：

∵AB∥CD,

∴∠BEF+∠DFE=180°.

∵EP为∠BEF的平分线，FP为∠EFD的平分线，

∴∠PEF=∠BEF,∠PFE=∠DFE.

∴∠PFE+∠PEF= (∠BEF+∠DFE)= ×180°=90°.

∴∠EPF=180°-(∠PEF+∠PFE)=90°.

∴△EFP为直角三角形.