题目内容
【题目】以下四个结论:
①一个多边形的内角和为900°,从这个多边形同一个顶点可画的对角线有4条;
②三角形的一个外角等于两个内角的和;
③任意一个三角形的三条高所在直线的交点一定在三角形的内部;
④△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形.
其中正确的是 (填序号)
【答案】①
【解析】结论①:设该多边形的边数为n (n为正整数且n>2),则![]() ,解得n=7.
,解得n=7.
因为从n边形(n为正整数且n>2)的同一个顶点最多可画(n-3)条对角线,
所以从这个多边形同一个顶点可画的对角线有7-3=4(条).故结论①正确.
结论②:因为三角形的一个外角等于与它不相邻的两个内角的和,而不是任意两个内角之和,故结论②错误.
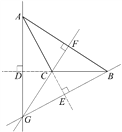
结论③:如图,△ABC为钝角三角形. 在△ABC中,三条高所在直线(即直线AD,BE,CF)的交点G在三角形外部,故结论③错误.
结论④:设∠A=(6x)°,根据∠A=2∠B=3∠C,则∠B=(3x)°,∠C=(2x)°.
在△ABC中,6x+3x+2x=11x=180,∴![]() ,
,
∴∠A,∠B,∠C均不等于90°.∴△ABC不是直角三角形.故结论④错误.
综上所述,正确的结论只有结论①.故本题应填写:① .

练习册系列答案
相关题目

