题目内容
【题目】在体育局的策划下，市体育馆将组织明星篮球赛，为此体育局推出两种购票方案（设购票张数为x，购票总价为y）：
方案一：提供8000元赞助后，每张票的票价为50元；
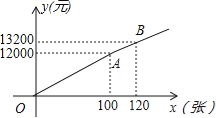
方案二：票价按图中的折线OAB所表示的函数关系确定．
（1）若购买120张票时，按方案一和方案二分别应付的购票款是多少？
（2）求方案二中y与x的函数关系式；
（3）至少买多少张票时选择方案一比较合算？
【答案】(1)14000,13200; （2）y=60x+6000．（3）200.
【解析】
试题（1）方案一中，总费用y=8000+50x，代入x=120求得答案；由图可知方案二中，当x=120时，对应的购票总价为13200元；
（2）分段考虑当0＜x≤100时，当x≥100时，设出一次函数解析式，把其中两点的坐标代入即可求得相应的函数解析式；
（3）由（1）（2）的解析式建立不等式，求得答案即可．
试题解析：（1）若购买120张票时，
方案一购票总价：y=8000+50x=14000元，
方案二购票总价：y=13200元．
（2）当0＜x≤100时，
设y=kx，代入（100，12000）得
12000=100k，
解得k=120，
∴y=120x；
当x＞100时，
设y=ax+b，代入（100，12000）、（120，13200）得
，
解得
，
∴y=60x+6000．
（3）由（1）可知，要选择方案一比较合算，必须超过120张，由此得
8000+50x≤60x+6000，
解得x≥200，
所以至少买200张票时选择方案一比较合算．
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作．已知该水果的进价为8元/千克，下面是他们在活动结束后的对话．
小丽：如果以10元/千克的价格销售，那么每天可售出300千克．
小强：如果每千克的利润为3元，那么每天可售出250千克．
小红：如果以13元/千克的价格销售，那么每天可获取利润750元．
【利润=（销售价-进价）
销售量】
（1）请根据他们的对话填写下表：
销售单价x（元/kg） | 10 | 11 | 13 |
销售量y（kg） |
（2）请你根据表格中的信息判断每天的销售量y（千克）与销售单价x（元）之间存在怎样的函数关系．并求y（千克）与x（元）（x＞0）的函数关系式；
（3）设该超市销售这种水果每天获取的利润为W元，求W与x的函数关系式．当销售单价为何值时，每天可获得的利润最大？最大利润是多少元？
