��Ŀ����
����Ŀ����ƽ�漸���У�����ѧ������ֱ��ƽ�еĶ��壬���������һ�κ�����ͼ����ȷ��������ֱ�ߣ���������ƽ�еĶ��壺��һ�κ���y=k1x+b1��k1��0����ͼ��Ϊֱ��l1��һ�κ���y=k2x+b2��k2��0����ͼ��Ϊֱ��l2����k1=k2����b1��b2�����Ǿͳ�ֱ��l1��ֱ��l2����ƽ�У������������⣺
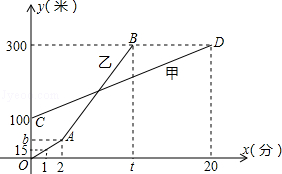
��1�������P��1��2����������ֱ֪��y=-2x-1ƽ�е�ֱ��l�ĺ�������ʽ��������ͼ��
��2����ֱ��l�ֱ���y�ᣬx�ύ�ڵ�A��B�����ֱ��m��y=kx+t��t��0����ֱ��lƽ�У��ҽ�x���ڵ�C�������ABC�����S������t������ϵʽ��
���𰸡���1��y=-2x+4;��2��S=![]() ��
��
��������
��1��ֱ��l����ֱ֪��y=-2x-1ƽ�У����ֱ��l��һ����ϵ����-2�����ݴ���ϵ�����Ϳ��������������ʽ��
��2�������A��B��������꣬�Ե�C��λ�÷���B��������Ҳ���������������ۣ��ٸ��������ε������ʽ�����ABC�����S����t�ĺ�������ʽ��
��1����ֱ��l�ĺ�������ʽΪy=kx+b��
��ֱ��l��ֱ��y=-2x-1ƽ�У���k=-2��
��ֱ��l��y=-2x+b����P��1��2����
��-2+b=2��
��b=4��
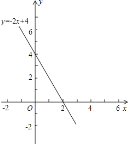
��ֱ��l�ĺ�������ʽΪy=-2x+4��
ֱ��l��ͼ����ͼ��
��2����ֱ��l�ֱ���y�ᡢx�ύ�ڵ�A��B��
���A��B������ֱ�Ϊ��0��4������2��0����
��l��m��
��ֱ��mΪy=-2x+t��
��y=0�����x=![]() ��
��
��C���������![]() ��0����
��0����
��t��0����![]() ��0��
��0��
��C����x����������ϣ�
��C����B������ʱ��S=![]() ����2-
����2-![]() ����4=4-t��
����4=4-t��
��C����B����Ҳ�ʱ��S=![]() ����
����![]() -2����4=t-4��
-2����4=t-4��
���ABC�����S����t�ĺ�������ʽΪS=![]() ��
��

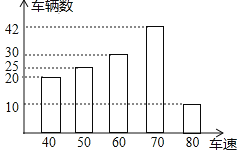
����Ŀ��С��ͬѧ��ѧУ��֯���������и����˽�������ס��С��450�������������ˮ��������������������50��������¾���ˮ��(��λ��t)����������������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ(��ͼ)��
(1)������������е���Ϣ��ȫƵ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
�¾���ˮ��/t | Ƶ�� | �ٷֱ� |
2��x��3 | 2 | 4% |
3��x��4 | 12 | 24% |
4��x��5 | ||
5��x��6 | 10 | 20% |
6��x��7 | 12% | |
7��x��8 | 3 | 6% |
8��x��9 | 2 | 4% |
 ��
��
(2)�����ͥ�¾���ˮ�������ڻ����4 t��С��7 t��Ϊ�е���ˮ����ͥ������ͨ���������������е��е���ˮ����ͥ��Լ�ж��ٻ���