题目内容
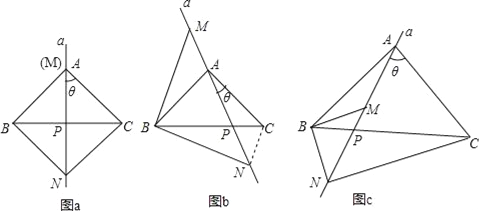
【题目】已知,在△ABC中,AB=AC.过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ,直线a交BC边于点P(点P不与点B、点C重合),△BMN的边MN始终在直线a上(点M在点N的上方),且BM=BN,连接CN.
(1)当∠BAC=∠MBN=90°时,
①如图a,当θ=45°时,∠ANC的度数为 ;
②如图b,当θ≠45°时,①中的结论是否发生变化?说明理由;
(2)如图c,当∠BAC=∠MBN≠90°时,请直接写出∠ANC与∠BAC之间的数量关系,不必证明.

【答案】(1)①45°;②当θ≠45°时,①中的结论不发生变化,理由见解析;(2)∠ANC=90°﹣![]() ∠BAC.
∠BAC.
【解析】试题分析:(1)①证明四边形ABNC是正方形,根据正方形的对角线平分一组对角线即可求解;
②根据等腰直角三角形的性质可得∠BNP=∠ACB,然后证明△BNP和△ACP相似,根据相似三角形对应边成比例可得![]() ,再根据两边对应成比例夹角相等可得△ABP和△CNP相似,然后根据相似三角形对应角相等可得∠ANC=∠ABC,从而得解;
,再根据两边对应成比例夹角相等可得△ABP和△CNP相似,然后根据相似三角形对应角相等可得∠ANC=∠ABC,从而得解;
(2)根据等腰三角形的两底角相等求出∠BNP=∠ACB,然后证明△BNP和△ACP相似,根据相似三角形对应边成比例可得![]() ,再根据两边对应成比例夹角相等可得△ABP和△CNP相似,然后根据相似三角形对应角相等可得∠ANC=∠ABC,然后根据三角形的内角和定理列式整理即可得解.
,再根据两边对应成比例夹角相等可得△ABP和△CNP相似,然后根据相似三角形对应角相等可得∠ANC=∠ABC,然后根据三角形的内角和定理列式整理即可得解.
试题解析:(1)①∵∠BAC=90°,θ=45°,∴AP⊥BC,BP=CP(等腰三角形三线合一),
∴AP=BP(直角三角形斜边上的中线等于斜边的一半),
又∵∠MBN=90°,BM=BN,∴AP=PN(等腰三角形三线合一),
∴AP=PN=BP=PC,且AN⊥BC,∴四边形ABNC是正方形,∴∠ANC=45°;
②连接CN,当θ≠45°时,①中的结论不发生变化.
理由如下:∵∠BAC=∠MBN=90°,AB=AC,BM=BN,∴∠ABC=∠ACB=∠BNP=45°,
又∵∠BPN=∠APC,∴△BNP∽△ACP,∴![]() ,
,
又∵∠APB=∠CPN,∴△ABP∽△CNP,
∴∠ANC=∠ABC=45°;
(2)∠ANC=90°﹣![]() ∠BAC.
∠BAC.
理由如下:∵∠BAC=∠MBN≠90°,AB=AC,BM=BN,
∴∠ABC=∠ACB=∠BNP=![]() (180°﹣∠BAC),
(180°﹣∠BAC),
又∵∠BPN=∠APC,∴△BNP∽△ACP,∴![]() ,
,
又∵∠APB=∠CPN,∴△ABP∽△CNP,∴∠ANC=∠ABC,
在△ABC中,∠ABC=![]() (180°﹣∠BAC)=90°﹣
(180°﹣∠BAC)=90°﹣![]() ∠BAC.
∠BAC.