题目内容
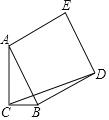
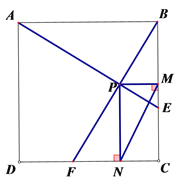
【题目】如图，四边形ABCD是边长为1的正方形，动点E、F分别从点C，D出发，以相同速度分别沿CB，DC运动（点E到达C时，两点同时停止运动）.连接AE，BF交于点P，过点P分别作PM∥CD，PN∥BC，则线段MN的长度的最小值为（ ）
A. 
B. 
C. 
D. 1
【答案】B
【解析】分析：由于点P在运动中保持∠APD=90°，所以点P的路径是一段以AD为直径的弧，设AD的中点为Q，连接QC交弧于点P，此时CP的长度最小，再由勾股定理可得QC的长，再求CP即可．
详解： 由于点P在运动中保持∠APD=90°， ∴点P的路径是一段以AD为直径的弧，
设AD的中点为Q，连接QC交弧于点P，此时CP的长度最小，
在Rt△QDC中，QC=
， ∴CP=QC－QP=
，故选B．
练习册系列答案
相关题目
【题目】
年
月
日是第
个世界读书日，为迎接第个世界读书日的到来，某校举办读书分享大赛活动：大赛以“推荐分享”为主题，参赛者选择一本自己最喜欢的书，然后给该书写一段推荐语、一篇读书心得、举办一场读书讲座．大赛组委会对参赛者提交的推荐语、读书心得、举办的读书讲座进行打分（各项成绩均按百分制），综合成绩排名第一的选手将获得大赛一等奖．现有甲、乙两位同学的各项成绩如下表所示；
参赛者 | 推荐语 | 读书心得 | 读书讲座 |
甲 |
|
|
|
乙 |
|
|
|
（1）若将三项成绩的平均分作为参赛选手的综合成绩，则甲、乙二人谁最有可能获得大赛一等奖？请通过计算说明理由．
（2）若“推荐语”“读书心得”“读书讲座”的成绩按
确定综合成绩，则甲、乙二人谁最有可能获得大赛一等奖？请通过计算说明理由．
