题目内容
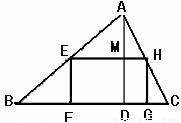
如图所示，一块三角形的余料，底边BC长1.8米，高AD=1米，要利用它裁剪一个长宽比是3：2的长方形，使长方形的长在BC上，另两个顶点在AB、AC上，求长方形的面积．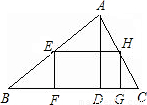
【答案】分析：由长方形的性质可推出△AEH∽△ABC，从而得出EH：BC=AM：AD，用x分别表示出EH和AM，代入上式，解出x的值，即可求出长方形的面积．
解答：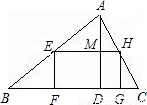
解：∵EH∥BC，
∴△AEH∽△ABC，
∴
，
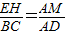设EH=3x，则EF=2x，
得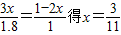
，
∴
．
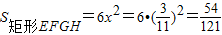点评：本题主要考查了平行线分线段成比例，相似三角形的判定与性质等知识点，根据平行得出的线段的比例关系来表示出相关的线段的长是解题的关键．
解答：
解：∵EH∥BC，∴△AEH∽△ABC，
∴
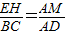，设EH=3x，则EF=2x，
得
，∴
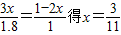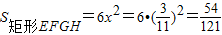．点评：本题主要考查了平行线分线段成比例，相似三角形的判定与性质等知识点，根据平行得出的线段的比例关系来表示出相关的线段的长是解题的关键．
练习册系列答案
相关题目
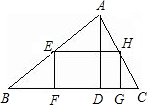如图所示，一块三角形的余料，底边BC长1.8米，高AD=1米，要利用它裁剪一个长宽比是3：2的长方形，使长方形的长在BC上，另两个顶点在AB、AC上，求长方形的面积．
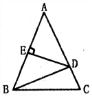20、如图所示是一块三角形田地，AB=AC=10m，AB的垂直平分线ED交AB于E，交AC于D，已量得△BDC的周长为16m，则BC的长为
