Question

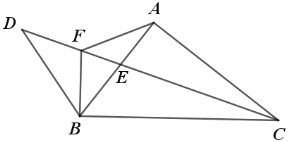
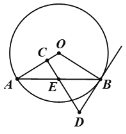
【题目】如图，AB是⊙O的弦，过AB的中点E作EC⊥OA于C，过点B作⊙O的切线BD交CE的延长线于点D．

（1）求证：DB=DE；

（2）连接AD，若AB=24，DB=10，求四边形OADB的面积．

Answer 1

【答案】（1）证明见解析；（2）四边形OADB的面积为

【解析】

（1）欲证明DB=DE，只要证明∠DEB=∠DBE；

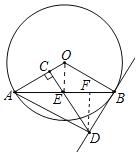
（2）作DF⊥AB于F，连接OE．只要证明∠AOE=∠DEF，可得sin∠DEF=sin∠AOE=由此求出AO的长，由勾股定理可求OE的长即可解决问题．

证明：（1）∵AO=OB，

∴∠OAB=∠OBA，

∵BD是切线，

∴OB⊥BD，

∴∠OBD=90°，

∴∠OBE+∠EBD=90°，

∵EC⊥OA，

∴∠CAE+∠CEA=90°，

∵∠CEA=∠DEB，

∴∠EBD=∠BED，

∴DB=DE．

（2）作DF⊥AB于F，连接OE．

∵DB=DE，AE=EB=12，

∴EF=BE=6，OE⊥AB，

在Rt△EDF中，DE=BD=10，EF=6，

∴DF=

∵∠AOE+∠OAB=90°，∠DEF+∠OAB=90°，

∴∠AOE=∠DEF，

∴sin∠DEF=sin∠AOE=

∵AE=12， ∴AO=15

∴OE=

∴四边形OADB的面积=