ЬтФПФкШн
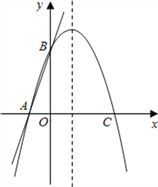
ЁОЬтФПЁПШчЭМЃЌжБЯпy=kx+bНЛxжсгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌНЛyжсгкЕуBЃЈ0ЃЌ4ЃЉЃЌЙ§AЁЂBСНЕуЕФХзЮяЯпНЛxжсгкСэвЛЕуCЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкИУХзЮяЯпЕФЖдГЦжсЩЯгавЛЖЏЕуPЃЌСЌНгPAЁЂPBЃЌШєВтЕУPA+PBЕФзюаЁжЕЮЊ5ЃЌЧѓДЫЪБХзЮяЯпЕФНтЮіЪНМАЕуPЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЬѕМўЯТЃЌдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕуQЃЌЪЙЁїABQЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌжБНгаДГіЗћКЯЬѕМўЕФЫљгаQЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=4x+4ЃЛЃЈ2ЃЉy=-![]() x2+
x2+![]() x+4ЃЌPЃЈ1ЃЌ
x+4ЃЌPЃЈ1ЃЌ![]() ЃЉЃЛЃЈ3ЃЉДцдкетбљЕФЕуQЃЌЪЙЁїABQЮЊЕШбќШ§НЧаЮЃЎQ1ЃЈ1ЃЌ
ЃЉЃЛЃЈ3ЃЉДцдкетбљЕФЕуQЃЌЪЙЁїABQЮЊЕШбќШ§НЧаЮЃЎQ1ЃЈ1ЃЌ![]() ЃЉЃЌQ2ЃЈ1ЃЌ0ЃЉЃЌQ3ЃЈ1ЃЌ
ЃЉЃЌQ2ЃЈ1ЃЌ0ЃЉЃЌQ3ЃЈ1ЃЌ![]() ЃЉЃЌQ4ЃЈ1ЃЌЉ
ЃЉЃЌQ4ЃЈ1ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉНЋЕуAЁЂBЕФзјБъДњШыжБЯпНтЮіЪНЃЌЧѓГіkЁЂbЕФжЕЃЌМЬЖјЕУГіжБЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНгBCЃЌдђBCгыЖдГЦжсЕФНЛЕуМДЪЧPЕуЕФЮЛжУЃЌИљОнPA+PBЕФзюаЁжЕЮЊ5ЃЌПЩЧѓГіOCЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓГіХзЮяЯпНтЮіЪНЃЌжБЯпBCНтЮіЪННјЖјЧѓГіЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЩшДцдкетбљЕФЕуQЃЌЦфзјБъЮЊЃЈ1ЃЌyЃЉЃЌШЛКѓЗжШ§жжЧщПіЬжТлЃЌЂйQA=QBЃЌЂкBA=BQЃЌЂлAB=AQЃЌЗжБ№ЧѓГіyЕФжЕКѓМДПЩЕУГіЕуQзјБъЃЎ
ЯъНтЃК(1)НЋЕуA(1ЃЌ0)ЃЌЕуB(0ЃЌ4)ДњШыжБЯпy=kx+b
ЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпABЕФНтЮіЪНЮЊy=4x+4ЃЛ
(2)ЁпЕуAЁЂЕуCЙигкХзЮяЯпЕФЖдГЦжсЖдГЦЃЌЙЪPA+PBЕФзюаЁжЕЮЊЯпЖЮBCЕФГЄЃЌ
ЁрBC=5ЃЌ
дкRtЁїBOCжаЃЌBC=5ЃЌBO=4ЃЌ
ЁрOC=![]() ЃЌ
ЃЌ
ЁрЕуCЕФзјБъЮЊ(3ЃЌ0)ЃЌ
ЩшХзЮяЯпЕФНтЮіЪНЮЊy=a(x+1)(x3)ЃЌ
НЋЕуB(0ЃЌ4)ДњШыЕУЃКa=![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃКy=![]() (x+1)(x3)=
(x+1)(x3)=![]() x2+
x2+![]() x+4ЃЛ
x+4ЃЛ
ЩшжБЯпBCЕФНтЮіЪНЮЊy=mx+nЃЌ
НЋЕуB(0ЃЌ4)ЃЌЕуC(3ЃЌ0)ДњШыПЩЕУЃЌ
![]() ЃЌ
ЃЌ
НтЕУЃК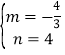 ЃЌ
ЃЌ
ЙЪжБЯпBCЕФНтЮіЪНЮЊЃКy=![]() x/span>+4ЃЌ
x/span>+4ЃЌ
гжЁпХзЮяЯпЕФЖдГЦжсЮЊx=1ЃЌ
ЁрЕБx=1ЪБЃЌy=![]() ЃЌ
ЃЌ
ЁрЕуPЕФзјБъЮЊ(1ЃЌ![]() ).
).
(3)ДцдкетбљЕФЕуQЃЌЪЙЁїABQЮЊЕШбќШ§НЧаЮ.
ЩшQ(1ЃЌy)ЃЌ
гаШ§жжЧщПіЃК
ЂйЕБQA=QBЪБЃЌдђга12+(y4)2=(11)2+y2ЃЌ
НтЕУЃКy=![]() ЃЌМДQ(1ЃЌ
ЃЌМДQ(1ЃЌ![]() )ЃЛ
)ЃЛ
ЂкЕБBA=BQЪБЃЌПЩжЊQ(1ЃЌ0)ЃЌQ(1ЃЌ8)(ВЛКЯЬтвтЃЌЩсШЅ)ЃЛ
ЂлЕБAB=AQЪБЃЌQ(1ЃЌ![]() )ЛђQ(1ЃЌ
)ЛђQ(1ЃЌ![]() ).
).
ЫљвдТњзуЬѕМўЕФQгаЫФИіЃКQ1ЃЈ1ЃЌ![]() ЃЉЃЌQ2ЃЈ1ЃЌ0ЃЉЃЌQ3ЃЈ1ЃЌ
ЃЉЃЌQ2ЃЈ1ЃЌ0ЃЉЃЌQ3ЃЈ1ЃЌ![]() ЃЉЃЌQ4ЃЈ1ЃЌЉ
ЃЉЃЌQ4ЃЈ1ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ

 ЦкФЉКУГЩМЈЯЕСаД№АИ
ЦкФЉКУГЩМЈЯЕСаД№АИ 99Мг1СьЯШЦкФЉЬибЕОэЯЕСаД№АИ
99Мг1СьЯШЦкФЉЬибЕОэЯЕСаД№АИ АйЧПУћаЃЦкФЉГхДЬ100ЗжЯЕСаД№АИ
АйЧПУћаЃЦкФЉГхДЬ100ЗжЯЕСаД№АИ КУГЩМЈ1Мг1ЦкФЉГхДЬ100ЗжЯЕСаД№АИ
КУГЩМЈ1Мг1ЦкФЉГхДЬ100ЗжЯЕСаД№АИ Н№зДдЊМЈгХКУОэЯЕСаД№АИ
Н№зДдЊМЈгХКУОэЯЕСаД№АИ