题目内容
(2002•哈尔滨)如图,△ABC内接于⊙O,BC=4,S△ABC=6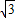 ,∠B为锐角,且关于x的方程x2-4xcosB+1=0有两个相等的实数根.D是劣弧
,∠B为锐角,且关于x的方程x2-4xcosB+1=0有两个相等的实数根.D是劣弧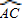 上任一点(点D不与点A、C重合),DE平分∠ADC,交⊙O于点E,交AC于点F.
上任一点(点D不与点A、C重合),DE平分∠ADC,交⊙O于点E,交AC于点F.(1)求∠B的度数;
(2)求CE的长;
(3)求证:DA、DC的长是方程y2-DE•y+DE•DF=0的两个实数根.
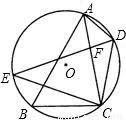
【答案】分析:(1)已知关于x的方程有两个相等的实数根,可根据根的判别式来得到cosB的值,进而判断出∠B的度数;
(2)在(1)题中不难得出∠B=60°,而四边形ABCD内接于⊙O,可得到∠ADE=∠CDE=∠B=60°,欲求CE,可先求出AC的长.过A作AG⊥BC于G,根据△ABC的面积和BC的长,可求得AG的值,进而通过解直角三角形可求出BG、CG的长,在Rt△AGC中,由勾股定理即可求得AC(即CE)的值;
(3)若DA、DC是所求方程的两个根,需满足两个条件:①DA+DC=DE,②DA•DC=DE•DF;
①可在DE上截取DM=DA,连接AE,通过证△AME≌△ADC,来得到EM=DC,从而得到DA+DC=DE;
②通过证△ADF∽△EDC来求得DA•DC=DE•DF.
得到上述两个条件后,即可根据根与系数的关系来证得所求的结论.
解答:(1)解:由题意知: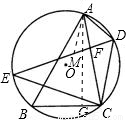
△=(4cosB)2-4=0,即cosB= ;
;
∴∠B=60°;
(2)解:过A作AG⊥BC于G;
∵S△ABC= BC•AG=6
BC•AG=6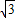 ,
,
∴AG=12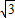 ÷4=3
÷4=3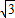 ;
;
Rt△ABG中,∠B=60°,AG=3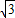 ,则BG=3;
,则BG=3;
Rt△AGC中,CG=BC-BG=1,AG=3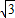 ,由勾股定理,得:
,由勾股定理,得:
AC= =2
=2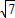 ;
;
∵四边形ABCD内接于⊙O,
∴∠ADC=180°-∠B=120°;
∵DE平分∠ADC,
∴∠EDC=∠EDA=∠B=60°;
∴EC=AC=2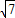 ;
;
(3)证明:在DE上截取DM=DA,连接AM;
由(2)知:∠EDA=60°,则△ADM是等边三角形,得:DA=DM=AM;
∵∠EDA=∠B=60°,
∴AE=AC;
∵∠EAC=∠EDC=∠MAD=60°,
∴∠EAM=∠DAC=60°-∠MAF;
又∵DA=AM,
∴△AME≌△ADC,得:EM=DC;
∴DE=EM+DM=DA+DC;…①
∵∠FAD=∠DEC,∠ADF=∠EDC,
∴△ADF∽△EDC;
∴DA•DC=DE•DF;…②
联立①②可知:DA、DC的长是方程y2-DE•y+DE•DF=0的两个实数根.
点评:此题考查了圆周角定理、三角形面积的求法、根与系数的关系、根的判别式、特殊角的三角函数值、解直角三角形、相似三角形及全等三角形的判定和性质等知识的综合应用能力,综合性强,难度较大.
(2)在(1)题中不难得出∠B=60°,而四边形ABCD内接于⊙O,可得到∠ADE=∠CDE=∠B=60°,欲求CE,可先求出AC的长.过A作AG⊥BC于G,根据△ABC的面积和BC的长,可求得AG的值,进而通过解直角三角形可求出BG、CG的长,在Rt△AGC中,由勾股定理即可求得AC(即CE)的值;
(3)若DA、DC是所求方程的两个根,需满足两个条件:①DA+DC=DE,②DA•DC=DE•DF;
①可在DE上截取DM=DA,连接AE,通过证△AME≌△ADC,来得到EM=DC,从而得到DA+DC=DE;
②通过证△ADF∽△EDC来求得DA•DC=DE•DF.
得到上述两个条件后,即可根据根与系数的关系来证得所求的结论.
解答:(1)解:由题意知:

△=(4cosB)2-4=0,即cosB=
 ;
;∴∠B=60°;
(2)解:过A作AG⊥BC于G;
∵S△ABC=
 BC•AG=6
BC•AG=6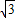 ,
,∴AG=12
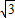 ÷4=3
÷4=3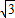 ;
;Rt△ABG中,∠B=60°,AG=3
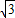 ,则BG=3;
,则BG=3;Rt△AGC中,CG=BC-BG=1,AG=3
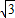 ,由勾股定理,得:
,由勾股定理,得:AC=
 =2
=2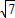 ;
;∵四边形ABCD内接于⊙O,
∴∠ADC=180°-∠B=120°;
∵DE平分∠ADC,
∴∠EDC=∠EDA=∠B=60°;
∴EC=AC=2
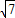 ;
;(3)证明:在DE上截取DM=DA,连接AM;
由(2)知:∠EDA=60°,则△ADM是等边三角形,得:DA=DM=AM;
∵∠EDA=∠B=60°,
∴AE=AC;
∵∠EAC=∠EDC=∠MAD=60°,
∴∠EAM=∠DAC=60°-∠MAF;
又∵DA=AM,
∴△AME≌△ADC,得:EM=DC;
∴DE=EM+DM=DA+DC;…①
∵∠FAD=∠DEC,∠ADF=∠EDC,
∴△ADF∽△EDC;
∴DA•DC=DE•DF;…②
联立①②可知:DA、DC的长是方程y2-DE•y+DE•DF=0的两个实数根.
点评:此题考查了圆周角定理、三角形面积的求法、根与系数的关系、根的判别式、特殊角的三角函数值、解直角三角形、相似三角形及全等三角形的判定和性质等知识的综合应用能力,综合性强,难度较大.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目


