题目内容
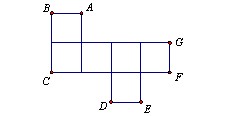
如图,△ABO中,OA=OB,以O为圆心的圆经过AB的中点C,分别交OA、OB于点E、F。若△ABO腰上的高BD等于底边AB的一半且AB=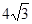 .
.
(1)求∠AOB的度数;
(2)求弧ECF的长;
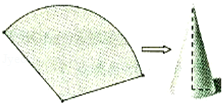
(3)把扇形OEF卷成一个无底的圆锥,则圆锥的底面半径是多少?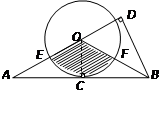
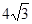 .
.(1)求∠AOB的度数;
(2)求弧ECF的长;
(3)把扇形OEF卷成一个无底的圆锥,则圆锥的底面半径是多少?

(1)∵△ABO腰上的高BD等于底边AB的一半
∴∠A=30°
∵OA=OB
∴∠ABO=30°
∴∠AOB=120°
(2)由(1)得∠A=30°
在Rt△ACO中,AC=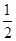 AB=2
AB=2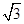 ,∠A=30°,
,∠A=30°,
则AO=2OC.
由勾股定理,求得OC=2.
∵∠AOB=120°.
由弧长公式可求得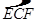 的长为
的长为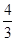 π.
π.
(3)r=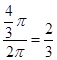
∴∠A=30°
∵OA=OB
∴∠ABO=30°
∴∠AOB=120°
(2)由(1)得∠A=30°
在Rt△ACO中,AC=
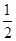 AB=2
AB=2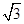 ,∠A=30°,
,∠A=30°,则AO=2OC.
由勾股定理,求得OC=2.
∵∠AOB=120°.
由弧长公式可求得
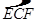 的长为
的长为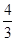 π.
π.(3)r=
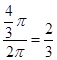
(1)利用直角三角形的角边关系得出∠A的度数,从而得出∠AOB的度数;
(2)利用勾股定律算出OC的长,然后根据弧长公式计算出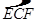 的长;
的长;
(3)利用圆锥底面圆的周长等于扇形的弧长算出圆锥的底面半径。
(2)利用勾股定律算出OC的长,然后根据弧长公式计算出
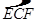 的长;
的长;(3)利用圆锥底面圆的周长等于扇形的弧长算出圆锥的底面半径。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
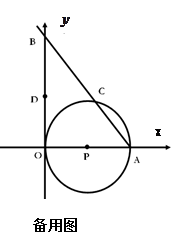
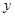 轴相切于坐标原点O(0,0),与
轴相切于坐标原点O(0,0),与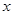 轴相交于点A(5,0),过点A的直线AB与
轴相交于点A(5,0),过点A的直线AB与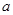 , D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同
, D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同 ,函数
,函数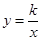 的图象经过点
的图象经过点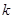 的值(用含
的值(用含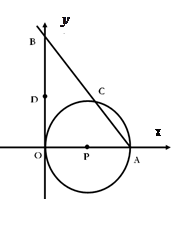
 半径为3cm,
半径为3cm,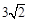
 cm
cm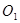 的半径为5
的半径为5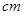 ,⊙
,⊙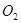 的半径为3
的半径为3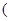
 外离
外离  外切
外切  内切
内切  相交
相交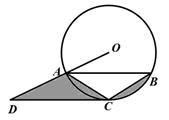
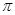 )
)