题目内容
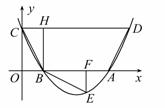
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于C点,且经过点
轴交于C点,且经过点![]() ,对称轴是直线
,对称轴是直线![]() ,顶点是
,顶点是![]() .
.
(1) 求抛物线对应的函数表达式;
(2) 经过![]() 两点作直线与
两点作直线与![]() 轴交于点
轴交于点![]() ,在抛物线上是否存在这样的点
,在抛物线上是否存在这样的点![]() ,使以点
,使以点![]() 为顶点的四边形为平行四边形?若存在,请求出点
为顶点的四边形为平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3) 设直线![]() 与y轴的交点是
与y轴的交点是![]() ,在线段
,在线段![]() 上任取一点
上任取一点![]() (不与
(不与![]() 重合),经过
重合),经过![]() 三点的圆交直线
三点的圆交直线![]() 于点
于点![]() ,试判断
,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(4) 当![]() 是直线
是直线![]() 上任意一点时,(3)中的结论是否成立?(请直接写出结论).
上任意一点时,(3)中的结论是否成立?(请直接写出结论).
 |
解:(1)根据题意,得
解得![]()
![]() 抛物线对应的函数表达式为
抛物线对应的函数表达式为![]() .
.
(2)存在.
在![]() 中,令
中,令![]() ,得
,得![]() .
.
令![]() ,得
,得![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
又![]() ,
,![]() 顶点
顶点![]() .
.
容易求得直线![]() 的表达式是
的表达式是![]() .
.
在![]() 中,令
中,令![]() ,得
,得![]() .
.
![]() ,
,![]() .
.
在![]() 中,令
中,令![]() ,得
,得![]() .
.
![]() .
.
![]() ,
,![]() 四边形
四边形![]() 为平行四边形,此时
为平行四边形,此时![]() .
.
(3)![]() 是等腰直角三角形.
是等腰直角三角形.
理由:在![]() 中,令
中,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() .
.
![]() 直线
直线![]() 与坐标轴的交点是
与坐标轴的交点是![]() ,
,![]() .
.
![]() ,
,![]() .
.
又![]() 点
点![]() ,
,![]() .
.![]() .
.
由图知![]() ,
,![]() .
.
![]() ,且
,且![]() .
.![]() 是等腰直角三角形.
是等腰直角三角形.
(4)当点![]() 是直线
是直线![]() 上任意一点时,(3)中的结论成立.
上任意一点时,(3)中的结论成立.
 |

练习册系列答案
相关题目
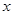 轴交于
轴交于 (2)点
(2)点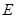 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以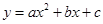 与
与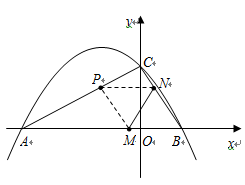
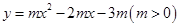 与
与 轴交于
轴交于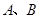 两点,与
两点,与 轴交于
轴交于 点.
点.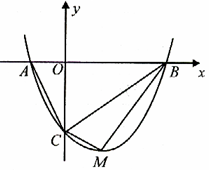
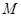 的坐标(用含
的坐标(用含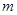 的代数式表示),
的代数式表示), 与
与 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;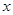 轴交于
轴交于 (
( ,0)、
,0)、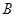 (
( ,0)两点,且
,0)两点,且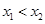 ,与
,与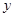 轴交于点
轴交于点 ,其中
,其中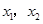 是方程
是方程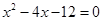 的两个根。(14分)
的两个根。(14分) (2)点
(2)点 是线段
是线段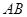 上的一个动点,过点
上的一个动点,过点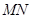 ∥
∥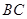 ,交
,交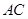 于点
于点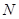 ,连接
,连接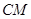 ,当
,当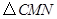 的面积最大时,求点
的面积最大时,求点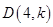 在(1)中抛物线上,
在(1)中抛物线上, 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以 为顶
为顶