题目内容
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2
,求⊙O的半径;
(3)若在⊙O上存在唯一点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径.

(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2
| 5 |
(3)若在⊙O上存在唯一点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径.

分析:(1)连接OB,求出∠OBP+∠ABP=90°,∠ACP+∠CPB=90°,∠OBP=∠OPB,推出∠ACP=∠ABC,根据等腰三角形的判定推出即可;
(2)延长AP交⊙O于D,连接BD,设圆半径为r,根据勾股定理得出AB2=OA2-OB2=52-r2,AC2=PC2-PA2=(2
)2-(5-r)2,根据AC=AB得出方程52-r2=(2
)2-(5-r)2,求出即可;
(3)作线段AC的垂直平分线MN,作OE⊥MN,求出OE=
.根据圆O要与直线MN有唯一交点,得出方程
=r,求出即可.
(2)延长AP交⊙O于D,连接BD,设圆半径为r,根据勾股定理得出AB2=OA2-OB2=52-r2,AC2=PC2-PA2=(2
| 5 |
| 5 |
(3)作线段AC的垂直平分线MN,作OE⊥MN,求出OE=
| 1 |
| 2 |
| 52-r2 |
| 1 |
| 2 |
| 52-r2 |
解答:解:(1)AB=AC.理由如下:如图1,
连接OB,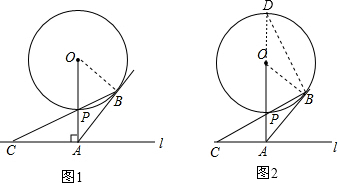
∵AB切⊙O于B,OA⊥AC,
∴∠OBA=∠OAC=90°,
∴∠OBP+∠ABP=90°,∠ACP+∠CPA=90°,
∵OP=OB,
∴∠OBP=∠OPB.
∵∠OPB=∠APC,
∴∠ACP=∠ABC,
∴AB=AC.
(2)如图2,
延长AP交⊙O于D,连接BD,
设圆半径为r,则由OA=5得,OP=OB=r,PA=5-r.
又∵PC=2
,
∴AB2=OA2-OB2=52-r2,AC2=PC2-PA2=(2
)2-(5-r)2,
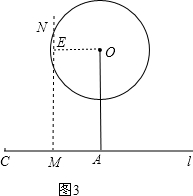 ∵由(1)知AC=AB,
∵由(1)知AC=AB,
∴52-r2=(2
)2-(5-r)2,
解得:r=3,
即⊙O的半径是3;
(3)作线段AC的垂直平分线MN,作OE⊥MN,
则OE=
AC=
AB=
.
又∵圆O要与直线MN有唯一交点,
∴OE=
=r,
∴r=
,
即⊙O的半径是
.
连接OB,
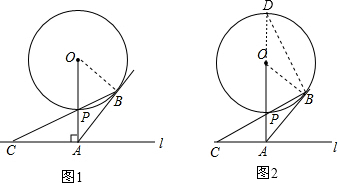
∵AB切⊙O于B,OA⊥AC,
∴∠OBA=∠OAC=90°,
∴∠OBP+∠ABP=90°,∠ACP+∠CPA=90°,
∵OP=OB,
∴∠OBP=∠OPB.
∵∠OPB=∠APC,
∴∠ACP=∠ABC,
∴AB=AC.
(2)如图2,
延长AP交⊙O于D,连接BD,
设圆半径为r,则由OA=5得,OP=OB=r,PA=5-r.
又∵PC=2
| 5 |
∴AB2=OA2-OB2=52-r2,AC2=PC2-PA2=(2
| 5 |
 ∵由(1)知AC=AB,
∵由(1)知AC=AB,∴52-r2=(2
| 5 |
解得:r=3,
即⊙O的半径是3;
(3)作线段AC的垂直平分线MN,作OE⊥MN,
则OE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 52-r2 |
又∵圆O要与直线MN有唯一交点,
∴OE=
| 1 |
| 2 |
| 52-r2 |
∴r=
| 5 |
即⊙O的半径是
| 5 |
点评:本题考查了切线的性质,等腰三角形的性质和判定,勾股定理,直线与圆的位置关系的应用,主要考查学生综合运用性质进行推理和计算的能力.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目

 26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°,
26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°,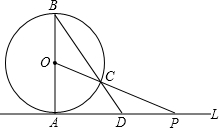 (1)若AP=4,求线段PC的长;
(1)若AP=4,求线段PC的长; 如图,已知直线AB与CD相交于点O,OE、OF分别是∠BOD、∠AOD的平分线.
如图,已知直线AB与CD相交于点O,OE、OF分别是∠BOD、∠AOD的平分线. 如图,已知直线l1与l2交于一点P,l1的函数表达式是y=2x+3,l2的函数表达式是y=kx+b(k≠0).点P的横坐标是-1,且l2与y轴的交点A的纵坐标也是-1.
如图,已知直线l1与l2交于一点P,l1的函数表达式是y=2x+3,l2的函数表达式是y=kx+b(k≠0).点P的横坐标是-1,且l2与y轴的交点A的纵坐标也是-1.