题目内容
如图,已知直线L与⊙O相切于点A,直径AB=6,点P在L上移动,连接OP交⊙O于点C,连接BC并延长BC交直线L于点D.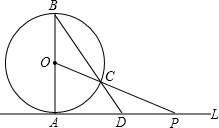 (1)若AP=4,求线段PC的长;
(1)若AP=4,求线段PC的长;(2)若△PAO与△BAD相似,求∠APO的度数和四边形OADC的面积(答案要求保留根号).
分析:(1)在Rt△OAP中,根据勾股定理可将OP的长求出,减去半径OC的长即为PC的长;
(2)如图,根据△PAO∽△BAD,可知∠2=∠APO,再根据∠1=2∠2,利用三角形的内角可将∠APO的度数求出;四边形OADC的面积可通过△ABD与△BOC的面积之差求得,也可由△OAP与△CDP的面积之差求得.
(2)如图,根据△PAO∽△BAD,可知∠2=∠APO,再根据∠1=2∠2,利用三角形的内角可将∠APO的度数求出;四边形OADC的面积可通过△ABD与△BOC的面积之差求得,也可由△OAP与△CDP的面积之差求得.
解答: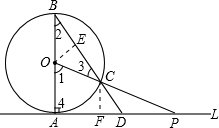 解:(1)∵l与⊙○相切于点A,
解:(1)∵l与⊙○相切于点A,
∴∠A=90°
∴OP2=OA2+AP2
∵OA=OC=
AB=3,AP=4
∴OP2=32+42
∴OP=5
∴PC=5-3=2;
(2)∵△PAO∽△BAD,且∠1>∠2,∠A=∠A=90°
∴∠2=∠APO.
又∠1=2∠2,∠A=90°,
∴∠1=2∠APO,
∴∠1+∠APO=90°
即3∠APO=90°
∴∠APO=30°
在Rt△BAD中,∠2=∠APO=30°
∴AD=6tan30°=6×
=2
方法一:过点O作OE⊥BC于点E
∵∠2=30°,BO=3
∴OE=
,BE=3×cos30°=
∴BC=2BE=3
∴S四边形OADC=S△BAD-S△BOC=
AB×AD-
BC×OE
=
×6×2
-
×3
×
=
;
方法二:在Rt△OAP中,AP=6tan60°=3
,OP=2OA=6
∴DP=AP-AD=3
-2
=
,PC=OP-OC=6-3=3
过点C作CF⊥AP于F
∵∠CPF=30°
∴CF=
PC=
∴S四边形OADC=S△OAP-S△CDP=
AP×OA-
DP×CF
=
(3
×3-
×
)
=
.
 解:(1)∵l与⊙○相切于点A,
解:(1)∵l与⊙○相切于点A,∴∠A=90°
∴OP2=OA2+AP2
∵OA=OC=
| 1 |
| 2 |
∴OP2=32+42
∴OP=5
∴PC=5-3=2;
(2)∵△PAO∽△BAD,且∠1>∠2,∠A=∠A=90°
∴∠2=∠APO.
又∠1=2∠2,∠A=90°,
∴∠1=2∠APO,
∴∠1+∠APO=90°
即3∠APO=90°
∴∠APO=30°
在Rt△BAD中,∠2=∠APO=30°
∴AD=6tan30°=6×
| ||
| 3 |
| 3 |
方法一:过点O作OE⊥BC于点E
∵∠2=30°,BO=3
∴OE=
| 3 |
| 2 |
3
| ||
| 2 |
∴BC=2BE=3
| 3 |
∴S四边形OADC=S△BAD-S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
=
| 15 |
| 4 |
| 3 |
方法二:在Rt△OAP中,AP=6tan60°=3
| 3 |
∴DP=AP-AD=3
| 3 |
| 3 |
| 3 |
过点C作CF⊥AP于F
∵∠CPF=30°
∴CF=
| 1 |
| 2 |
| 3 |
| 2 |
∴S四边形OADC=S△OAP-S△CDP=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
=
15
| ||
| 4 |
点评:此题考查了勾股定理的计算,相似三角形的性质与判定,不规则图形的面积的计算等知识,综合性比较强,其中不规则图形的面积可通过几个规则图形面积相加或相减求得.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目

 26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°,
26、如图,已知直线AB与CD相交于点O,OB平分∠EOD,∠1+∠2=90°,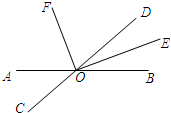 如图,已知直线AB与CD相交于点O,OE、OF分别是∠BOD、∠AOD的平分线.
如图,已知直线AB与CD相交于点O,OE、OF分别是∠BOD、∠AOD的平分线.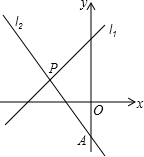 如图,已知直线l1与l2交于一点P,l1的函数表达式是y=2x+3,l2的函数表达式是y=kx+b(k≠0).点P的横坐标是-1,且l2与y轴的交点A的纵坐标也是-1.
如图,已知直线l1与l2交于一点P,l1的函数表达式是y=2x+3,l2的函数表达式是y=kx+b(k≠0).点P的横坐标是-1,且l2与y轴的交点A的纵坐标也是-1.