题目内容
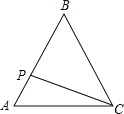
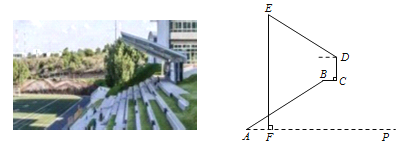
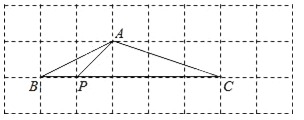
【题目】阅读下面材料:小明遇到一个问题:如图,∠MON,点A在射线OM上,点B在∠MON内部,用直尺和圆规作点P,使点P同时满足下列两个条件(要求保留作图痕迹,不必写出作法):
a.点P到A,B两点的距离相等;b.点P到∠MON的两边的距离相等.
小明的作法是:
①连接AB,作线段AB的垂直平分线交AB于E,交ON于F;
②作∠MON的平分线交EF于点P.
所以点P即为所求.
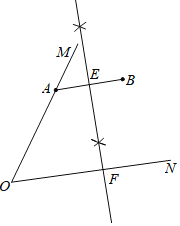
根据小明的尺规作图过程,
(1)使用直尺和圆规,补全图形;
(2)证明:∵EF垂直平分线段AB,点P在直线EF上,
∴PA= .
∵OP平分∠MON,
∴点P到∠MON的两边的距离相等 (填推理的依据).所以点P即为所求.
【答案】(1)见解析;(2)PB,角平分线上的点到角两边的距离相等.
【解析】
(1)利用基本作图方法,作∠MON的平分线OP即可;
(2)先根据线段垂直平分线的性质得到PA=PB,再根据角平分线的性质得到点P到∠MON的两边的距离相等,从而判断P点满足条件.
(1)解:如图,
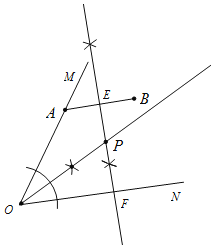
(2)证明:∵EF垂直平分线段AB,点P在直线EF上,
∴PA=PB.
∵OP平分∠MON,
∴点P到∠MON的两边的距离相等(角平分线上的点到角两边的距离相等).
所以点P即为所求.
故答案为PB;角平分线上的点到角两边的距离相等.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】下表,是池州市今年“五一”这周内日最高气温的统计表,关于这7天的日最高气温的众数,中位数,方差分别是:( )
日期 | 29日 | 30日 | 5月1日 | 2日 | 3日 | 4日 | 5日 |
日最高气温 | 16°C | 19°C | 22°C | 24°C | 26°C | 24°C | 23°C |
A. 24,23,10B. 24,23,![]() C. 24,22,10D. 24,22,
C. 24,22,10D. 24,22,![]()
【题目】某校要从小明和小亮两名运动员中挑出一人参加立定跳远比赛,学校记录了二人在最近的6次立定跳远选拔赛中的成绩(单位:cm),并进行整理、描述和分析.下面给出了部分信息.
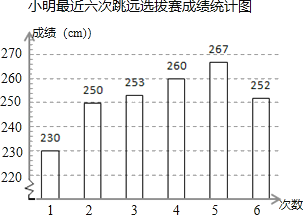
a.如图
b.小亮最近6次选拔赛成绩如下:
250 | 254 | 260 | 271 | 255 | 240 |
c.小明和小亮最近6次选拔赛中成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
小明 | 252 | 252.5 | 129.7 |
小亮 | 255 | m | 88.7 |
根据以上信息,回答下列问题:
(1)m= ;
(2)历届比赛表明:成绩达到266cm就有可能夺冠,成绩达到270cm就能打破纪录(积分加倍),根据这6次选拔赛成绩,你认为应选 (填“小明”或“小亮”)参加这项比赛,理由是 .(至少从两个不同的角度说明推断的合理性)