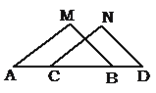
��Ŀ����
����Ŀ�����ı���ABCD�ı�AB��BC��CD��DAΪб�߷ֱ������������ֱ�������Σ�ֱ�Ƕ���ֱ�ΪE��F��G��H��˳���������ĸ��㣬���ı���EFGH��
��1����ͼ1�����ı���ABCDΪ������ʱ�����Ƿ����ı���EFGH�������Σ���ͼ2�����ı���ABCDΪ����ʱ�����жϣ��ı���EFGH����״����Ҫ��֤������
��2����ͼ3�����ı���ABCDΪһ��ƽ���ı���ʱ������ADC=����0��������90������
�����ú����Ĵ���ʽ��ʾ��HAE��
����֤��HE=HG��
���ı���EFGH��ʲô�ı��Σ���˵�����ɣ�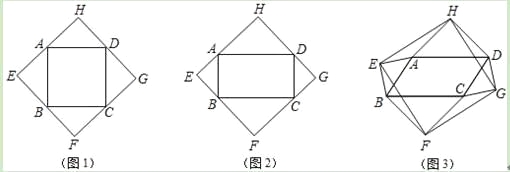
���𰸡���1�����ı���EFGH����״�������Σ�
��2���⣺�١�HAE=90��+a��
��ƽ���ı���ABCD��AB��CD��
���BAD=180�㩁��ADC=180�㩁a��
�ߡ�HAD����EAB�ǵ���ֱ�������Σ�
���HAD=��EAB=45����
���HAE=360�㩁��HAD����EAB����BAD=360�㩁45�㩁45�㩁��180�㩁a��=90��+a��
���ú����Ĵ���ʽ��ʾ��HAE��90��+a��
��֤�����ߡ�AEB����DGC�ǵ���ֱ�������Σ�
��AE=![]() AB��DC=
AB��DC=![]() CD��
CD��
��ƽ���ı���ABCD�У�AB=CD��
��AE=DG��
�ߡ�HAD����GDC�ǵ���ֱ�������Σ�
���HDA=��CDG=45����
���HDG=��HDA+��ADC+��CDG=90��+a=��HAE��
�ߡ�HAD�ǵ���ֱ�������Σ�
��HA=HD��
���HAE�ա�HDC��
��HE=HG��
�����ı���EFGH�������Σ�
�����ǣ�����ͬ���ɵã�GH=GF��FG=FE��
��HE=HG��
��GH=GF=EF=HE��
���ı���EFGH�����Σ�
�ߡ�HAE�ա�HDG��
���DHG=��AHE��
�ߡ�AHD=��AHG+��DHG=90����
���EHG=��AHG+��AHE=90����
���ı���EFGH�������Σ�
����������

����Ŀ����֪ij��Ʒ�Ľ���Ϊÿ��30Ԫ���ţ�1������ѧ��ȤС�龭���г����飬����������Ʒ�ڵ�x��1��x��90������ۼ��������������Ϣ���±���
��x�� | 1��x��50 | 50��x��90 |
�ۼۣ�Ԫ/���� | x��40 | 90 |
ÿ������������ | 200��2x | |
��1���ֱ������25��͵�60���̼������۸���Ʒʱ����õ�����
��2�������۸���Ʒ�ڼ���ʱ���������������Ϊ6050Ԫ��