题目内容
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论: ①AE=CF;
②△EPF是等腰直角三角形;
③S四边形AEPF= ![]() S△ABC;
S△ABC;
④当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合) BE+CF=EF.
上述结论中始终正确的有( )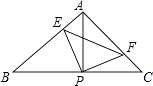
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:∵∠APE、∠CPF都是∠APF的余角, ∴∠APE=∠CPF,
∵AB=AC,∠BAC=90°,P是BC中点,
∴AP=CP,
又∵AP=CP,∠EPA=∠FPC,∠EAP=∠FCP=45°
∴△APE≌△CPF(ASA),同理可证△APF≌△BPE,
∴AE=CF,△EPF是等腰直角三角形,S四边形AEPF= ![]() S△ABC , ①②③正确;
S△ABC , ①②③正确;
故AE=FC,BE=AF,
∴AF+AE>EF,
∴BE+CF>EF,故④不成立.
始终正确的是①②③.故选C.
【考点精析】通过灵活运用等腰直角三角形和旋转的性质,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目