题目内容
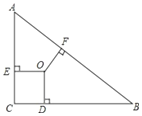
【题目】已知,在△ABC中,∠ABC=90,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D.E.F是垂足,且AB=17,BC=15,则OF、OE、OD的长度分别是( )
A. 2,2,2 B. 3,3,3 C. 4,4,4 D. 5,5,5
【答案】B
【解析】
由角平分线的性质易得OE=OF=OD,AE=AF,CE=CD,BD=BF,设OE=OF=OD=x,则CE=CD=x,BD=BF=15-x,AF=AE=8-x,所以15-x+8-x=17,解答即可.
解:如图,
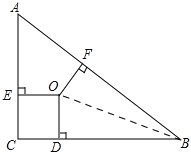
连接OB,
∵点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,
∴OE=OF=OD,
又∵OB是公共边,
∴Rt△BOF≌Rt△BOD(HL),
∴BD=BF,
同理,AE=AF,CE=CD,
∵∠C=90°,OD⊥BC,OE⊥AC,OF⊥AB,OD=OE,
∴OECD是正方形,
设OE=OF=OD=x,则CE=CD=x,BD=BF=15-x,AF=AE=8-x,
所以15-x+8-x=17
解得x=3.
则OE=OF=OD=3,
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某水果批发市场规定,一次购买苹果不超过100kg(包括100kg),批发价为5元,如果一次购买100kg以上苹果,超过100kg的部分苹果价格打8折.
(I)请填写下表
购买量/kg | 0 | 50 | 100 | 150 | 200 | … |
付款金额/元 | 0 | 250 | _ | 700 | __ | … |
(Ⅱ)写出付款金额关于购买量的函数解析式;
(Ⅲ)如果某人付款2100元,求其购买苹果的数量.